题目内容
函数f（x）=
+3（x＞0）的最小值是（ ）
| x3+x |
| x2 |
| A、5 | |||
B、3
| |||
| C、3 | |||
| D、2 |
考点：函数的最值及其几何意义
专题：计算题,不等式的解法及应用
分析：f（x）=
+3=x+
+3，利用基本不等式，即可得出结论．
| x3+x |
| x2 |
| 1 |
| x |
解答：
解：f（x）=
+3=x+
+3，
∵x＞0，∴x+
≥2（当且仅当x=1时取等号），
∴当x=1时，函数f（x）=
+3（x＞0）的最小值是2+3=5．
故选：A．
| x3+x |
| x2 |
| 1 |
| x |
∵x＞0，∴x+
| 1 |
| x |
∴当x=1时，函数f（x）=
| x3+x |
| x2 |
故选：A．
点评：本题考查函数的最值，考查基本不等式的运用，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
把4个颜色各不相同的乒乓球随机地放入编号为1、2、3、4的四个盒子里，则恰好有一个盒子是空盒的放法是（ ）种．
| A、64 | B、288 |
| C、256 | D、144 |
甲、乙两人下棋，两人下成和棋的概率是
，乙获胜的概率是
，则下列说法正确的是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、乙不输的概率是
| ||
B、甲获胜的概率是
| ||
C、甲不x=10输的概率是
| ||
D、乙输的概率是
|
在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别是棱A1D1，C1D1的中点，N为线段B1C的中点，若点P，M分别为线段D1B，EF上的动点，则PM+PN的最小值为（ ）
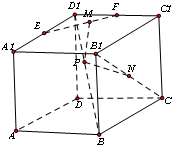
| A、1 | ||||||
B、
| ||||||
C、
| ||||||
D、
|
若两条异面直线所成的角为60°，则称这对异面直线为“黄金异面直线对”，在连接正方体的各个顶点的所有直线中，“黄金异面直线对”共有（ ）| A、12对 | B、18对 |
| C、24对 | D、30对 |
对于函数f（x），若?a，b，c∈R，f（a），f（b），f（c）都是某一三角形的三边长，则称f（x）为“保三角形函数”．以下说法正确的是（ ）
| A、f（x）=1（x∈R）不是“保三角形函数” | ||
B、若定义在R上的函数f（x）的值域是[
| ||
C、f（x）=
| ||
| D、“保三角形函数”一定是单调函数 |
若a=1.70.3，b=0.93.1，c=log30.7，则a，b，c的大小关系是（ ）
| A、a＞b＞c |
| B、a＞c＞b |
| C、b＞c＞a |
| D、c＞b＞a |