题目内容
设
=(x,4,3),
=(3,2,z),且
∥
,则xz等于 .
| a |
| b |
| a |
| b |
考点:共线向量与共面向量
专题:空间向量及应用
分析:利用空间向量平行的性质求解.
解答:
解:∵
=(x,4,3),
=(3,2,z),且
∥
,
∴
=
=
,
∴x=6,z=
,
∴xz=6×
=9.
故答案为:9.
| a |
| b |
| a |
| b |
∴
| x |
| 3 |
| 4 |
| 2 |
| 3 |
| z |
∴x=6,z=
| 3 |
| 2 |
∴xz=6×
| 3 |
| 2 |
故答案为:9.
点评:本题考查两个实数的积的求法,是基础题,解题时要认真审题,注意空间向量平行的性质的合理运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
边长为1的正三角形ABC中,向量
与
的数量积的值为( )
| AB |
| CB |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
命题“x<1”是命题“x≤1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
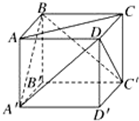 若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有( )
若两条异面直线所成的角为60°,则称这对异面直线为“黄金异面直线对”,在连接正方体的各个顶点的所有直线中,“黄金异面直线对”共有( )| A、12对 | B、18对 |
| C、24对 | D、30对 |
 一个正方体的六个面上分别标有A,B,C,D,E,F,如图是正方体的两种不同放置,则与D面相对的面上的字母是
一个正方体的六个面上分别标有A,B,C,D,E,F,如图是正方体的两种不同放置,则与D面相对的面上的字母是