题目内容
设A={-3,4},B={x|x2-2ax+b=0},B≠∅,且A∩B=B,求a,b的值.
考点:交集及其运算
专题:集合
分析:由A∩B=B得,B⊆A,由题设条件知B={-3}或B={4}或B={-3,4},再根据韦达定理、已知的方程,分别进行求解即可.
解答:
解:由A∩B=B得,B⊆A,
因为A={-3,4},B={x|x2-2ax+b=0}≠∅,且B⊆A,
所以B={-3}或B={4}或B={-3,4},
即x2-2ax+b=0的两根为-3,4,或有重根-3,4,
当B={-3}时,则
,解得a=-3,b=9;
当B={4}时,则
,解得a=4,b=16;
当B={-3,4}时,则
,解得a=
,b=-12,
综上得,
或
或
.
因为A={-3,4},B={x|x2-2ax+b=0}≠∅,且B⊆A,
所以B={-3}或B={4}或B={-3,4},
即x2-2ax+b=0的两根为-3,4,或有重根-3,4,
当B={-3}时,则
|
当B={4}时,则
|
当B={-3,4}时,则
|
| 1 |
| 2 |
综上得,
|
|
|
点评:本题考查集合的包含关系的判断和应用,以及韦达定理的运用,注意分类讨论思想的合理应用.

练习册系列答案
相关题目
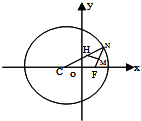 已知点C为圆(x+1)2+y2=8的圆心,N是圆上的动点,点H在圆的半径CN上,且有点F(1,0)和FN上的点M,满足
已知点C为圆(x+1)2+y2=8的圆心,N是圆上的动点,点H在圆的半径CN上,且有点F(1,0)和FN上的点M,满足