题目内容
已知函数f(x)=x3+x
,若不等式f(4x-m•2x+1)-f(4-x-m•2-x+1)≥0恒成立,则实数m的取值范围是( )
| 1 |
| 3 |
A、m≤
| ||
B、m≥
| ||
| C、m≤1 | ||
| D、m≥1 |
考点:函数的单调性与导数的关系
专题:导数的综合应用
分析:通过求f′(x)判断出f(x)在R上是增函数,所以由原不等式可得4x-m•2x+1≥4-x-m•2-x+1,该不等式又可变成4x-4-x≥m(2x+1-2-x+1),所以要求m的取值范围需讨论2x+1-2-x+1是否为0:x=0时,上面不等式成立;x≠0时,上面不等式变成m≤
,而
≥1,所以m≤1,这样即求出了m的范围.
| 2x+2-x |
| 2 |
| 2x+2-x |
| 2 |
解答:
解:f′(x)=3x2+
x-
>0;
∴f(x)在R上是增函数;
由原不等式得f(4x-m•2x+1)≥f(4-x-m•2-x+1);
∴4x-m•2x+1≥4-x-m•2-x+1;
∴4x-4-x≥m(2x+1-2-x+1),
①x=0时对任意m∈R上面不等式都成立;
②x≠0时上面不等式变成m≤
;
2x+2-x≥2,∴
≥1;
∴m≤1;
∴实数m的取值范围是(-∞,1].
故选:C.
| 1 |
| 3 |
| 2 |
| 3 |
∴f(x)在R上是增函数;
由原不等式得f(4x-m•2x+1)≥f(4-x-m•2-x+1);
∴4x-m•2x+1≥4-x-m•2-x+1;
∴4x-4-x≥m(2x+1-2-x+1),
①x=0时对任意m∈R上面不等式都成立;
②x≠0时上面不等式变成m≤
| 2x+2-x |
| 2 |
2x+2-x≥2,∴
| 2x+2-x |
| 2 |
∴m≤1;
∴实数m的取值范围是(-∞,1].
故选:C.
点评:考查根据导数符号判断函数的单调性的方法,对增函数定义的运用,平方差公式以及基本不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将两个数A=6,B=5交换,使A=5,B=6,使用赋值语句正确的一组( )
| A、C=B,B=A,A=C |
| B、A=B,B=A |
| C、B=A,A=B |
| D、A=C,C=B,B=A |
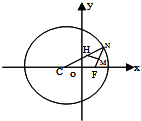 已知点C为圆(x+1)2+y2=8的圆心,N是圆上的动点,点H在圆的半径CN上,且有点F(1,0)和FN上的点M,满足
已知点C为圆(x+1)2+y2=8的圆心,N是圆上的动点,点H在圆的半径CN上,且有点F(1,0)和FN上的点M,满足