题目内容
已知命题p:2x2-3x+1≤0,q:(x-a)(x-a-1)>0,若p是¬q的充分不必要条件,求a的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:计算题,不等式的解法及应用,简易逻辑
分析:解出二次不等式,由p是¬q的充分不必要条件,即有[
,1]?[a,a+1],列出a的不等式,解出即可得到范围.
| 1 |
| 2 |
解答:
解:由2x2-3x+1≤0解得,
≤x≤1,
由(x-a)(x-a-1)>0解得,x>a+1,或x<a,
由于p是¬q的充分不必要条件,即有[
,1]?[a,a+1],
则a≤
且a+1≥1,解得,0≤a≤
.
即a的取值范围是[0,
].
| 1 |
| 2 |
由(x-a)(x-a-1)>0解得,x>a+1,或x<a,
由于p是¬q的充分不必要条件,即有[
| 1 |
| 2 |
则a≤
| 1 |
| 2 |
| 1 |
| 2 |
即a的取值范围是[0,
| 1 |
| 2 |
点评:本题考查充分必要条件的运用,考查不等式的解法和集合的包含关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某几何体的三视图如图所示,则此几何体的体积等于( )


| A、30 | B、12 | C、24 | D、4 |
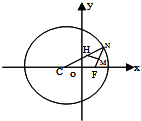 已知点C为圆(x+1)2+y2=8的圆心,N是圆上的动点,点H在圆的半径CN上,且有点F(1,0)和FN上的点M,满足
已知点C为圆(x+1)2+y2=8的圆心,N是圆上的动点,点H在圆的半径CN上,且有点F(1,0)和FN上的点M,满足