题目内容
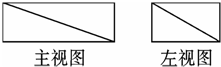
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,则f(0)的值为( )


| A、1 | ||
| B、0 | ||
C、
| ||
D、
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:利用y=Asin(ωx+φ)的部分图象可确定A,T,继而可求得ω=2,利用曲线经过(
,2),可求得φ,从而可得函数解析式,继而可求得答案.
| π |
| 2 |
解答:
解:由图知,A=2,
T=
-
=
,
∴T=
=π,解得ω=2,
又
×2+φ=2kπ+
(k∈Z),
∴φ=2kπ+
(k∈Z),0<φ<π,
∴φ=
,
∴f(x)=2sin(2x+
),
∴f(0)=2sin
=1.
故选:A.
| 3 |
| 4 |
| 11π |
| 12 |
| π |
| 6 |
| 3π |
| 4 |
∴T=
| 2π |
| ω |
又
| π |
| 6 |
| π |
| 2 |
∴φ=2kπ+
| π |
| 6 |
∴φ=
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
∴f(0)=2sin
| π |
| 6 |
故选:A.
点评:本题考查利用y=Asin(ωx+φ)的部分图象确定解析式,φ的确定是关键,考查识图与运算能力,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知x=log3e,y=log97,z=e
,则( )
| 1 |
| 2 |
| A、x>y>z |
| B、y>z>x |
| C、z>y>x |
| D、z>x>y |
已知函数f(x)=|log2(x-1)|-(
)x有两个零点x1,x2,则( )
| 1 |
| 3 |
| A、x1x2<1 |
| B、x1x2>x1+x2 |
| C、x1x2=x1+x2 |
| D、x1x2<x1+x2 |
下列命题中正确的是( )
| A、命题“若x2-5x+6=0,则x=2”的逆命题是“若x≠2,则x2-5x+6≠0” | |||||||||
| B、对命题p:?x∈R,使得x2+x+1<0,则?p:?x∈R,则x2+x+1<0 | |||||||||
C、着实数x,y∈[0,1],则满足
| |||||||||
D、已知a=
|
已知
=a+i(a,b∈R),其中i为虚数单位,则a+b=( )
| 1-bi |
| 1+2i |
| A、-4 | B、4 | C、-10 | D、10 |
集合A={y|y=lgx,x>1},B={-2,-1,1,2},则∁RA∩B=( )
| A、[-2,-1] |
| B、(-∞,0] |
| C、{1,2} |
| D、{-2,-1} |
若集合A={y|0≤y<2},B={x|-1<x<1},则A∩(∁RB)=( )
| A、{x|0≤x≤1} |
| B、{x|1≤x<2} |
| C、{x|-1<x≤0} |
| D、{x|0≤x<1} |

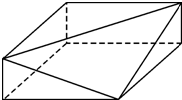 某几何体的直观图如图所示,该几何体的主(正)视图和左(侧)视图都正确的是( )
某几何体的直观图如图所示,该几何体的主(正)视图和左(侧)视图都正确的是( )