题目内容
20.在平面直角坐标系中,方程x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{{x}^{′}=2x}\\{{y}^{′}=3y}\end{array}\right.$后,得到的方程为( )| A. | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{3}$=1 | B. | 2x2+3y2=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 | D. | 4x2+9y2=1 |
分析 根据题意,由伸缩变换$\left\{\begin{array}{l}{{x}^{′}=2x}\\{{y}^{′}=3y}\end{array}\right.$可得$\left\{\begin{array}{l}{x=\frac{x′}{2}}\\{y=\frac{y′}{3}}\end{array}\right.$,将其代入方程x2+y2=1,进而化简即可得答案.
解答 解:根据题意,由伸缩变换$\left\{\begin{array}{l}{{x}^{′}=2x}\\{{y}^{′}=3y}\end{array}\right.$可得$\left\{\begin{array}{l}{x=\frac{x′}{2}}\\{y=\frac{y′}{3}}\end{array}\right.$,
将其代入方程x2+y2=1可得:($\frac{x′}{2}$)2+($\frac{y′}{3}$)2=1,
化简可得:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1;
故选:C.
点评 本题考查直角坐标系中的伸缩变化,关键是掌握伸缩变化的公式.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
12.执行如图所示的程序框图,则输出m的值为( )
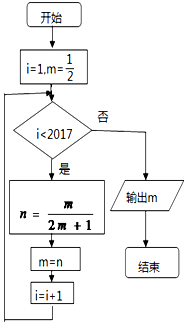

| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{4032}$ | D. | $\frac{1}{4034}$ |
9.读程序:

则运行程序后输出结果判断正确的是( )

则运行程序后输出结果判断正确的是( )
| A. | $S=\frac{100}{101},P=\frac{100}{101}$ | B. | $S=\frac{99}{100},P=\frac{99}{202}$ | ||
| C. | $S=\frac{100}{101},P=\frac{99}{202}$ | D. | $S=\frac{100}{101},P=\frac{99}{100}$ |
 已知底面为正方形的四棱锥P-ABCD,如图(1)所示,PC⊥面ABCD,其中图(2)为该四棱锥的正(主)视图和侧(左)视图,它们是腰长为4cm的全等的等腰直角三角形.
已知底面为正方形的四棱锥P-ABCD,如图(1)所示,PC⊥面ABCD,其中图(2)为该四棱锥的正(主)视图和侧(左)视图,它们是腰长为4cm的全等的等腰直角三角形. 如图,已知正方体ABC-A1B1C1D1中,AB=a,P为线段BC1上一点,Q为平面ABCD内一点,则D1P+PQ的最小值为(1+$\frac{\sqrt{2}}{2}$)a.
如图,已知正方体ABC-A1B1C1D1中,AB=a,P为线段BC1上一点,Q为平面ABCD内一点,则D1P+PQ的最小值为(1+$\frac{\sqrt{2}}{2}$)a.