题目内容
11.以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=lny,将其变换后得到线性方程z=0.3x+4,则c,k的值分别是e4和0.3.分析 我们根据对数的运算性质:loga(MN)=logaM+logaN,logaNn=nlogaN,即可得出结论.
解答 解:∵y=cekx,
∴两边取对数,可得lny=ln(cekx)=lnc+lnekx=lnc+kx,
令z=lny,可得z=lnc+kx,
∵z=0.3x+4,
∴lnc=4,k=0.3
∴c=e4.
故答案为:e4,0.3.
点评 本题考查的知识点是线性回归方程,其中熟练掌握对数的运算性质,是解答此类问题的关键.

练习册系列答案
相关题目
2.某几何体的三视图如图所示,则此几何体的外接球的表面积为( )


| A. | 8π | B. | 13π | C. | 17π | D. | 48π |
20.在平面直角坐标系中,方程x2+y2=1经过伸缩变换$\left\{\begin{array}{l}{{x}^{′}=2x}\\{{y}^{′}=3y}\end{array}\right.$后,得到的方程为( )
| A. | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{3}$=1 | B. | 2x2+3y2=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 | D. | 4x2+9y2=1 |
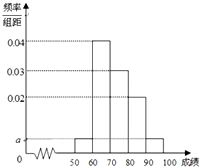 某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
某校100名学生期末考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 小晶用圆、三角形、正方形按一定规律画图,前八个图形如图所示,则猜测第2017个图形中共含有的正方形个数为336.
小晶用圆、三角形、正方形按一定规律画图,前八个图形如图所示,则猜测第2017个图形中共含有的正方形个数为336.