题目内容
已知函数f(x)=x3-3a2x2-2ax,x∈[0,1],且a≥1.
(Ⅰ)判断函数f(x)的单调性并予以证明;
(Ⅱ)若函数f(x)的值域为A,且[-4,-3]⊆A,求实数a的取值范围.
(Ⅰ)判断函数f(x)的单调性并予以证明;
(Ⅱ)若函数f(x)的值域为A,且[-4,-3]⊆A,求实数a的取值范围.
考点:函数单调性的判断与证明,函数单调性的性质
专题:函数的性质及应用
分析:(Ⅰ)直接根据函数单调性的定义进行求证即可;
(Ⅱ)结合函数的单调性和集合的包含关系进行求解.
(Ⅱ)结合函数的单调性和集合的包含关系进行求解.
解答:
解:(Ⅰ)设x1,x2∈[0,1],x1<x2,
∴f(x1)-f(x2)
=x13-3a2x12-2ax1-(x23-3a2x22-2ax2)
=(x1-x2)(x12+x1x2+x22-3a2)>0,
∴f(x)单调递减.
(Ⅱ)由函数f(x)的值域为:
1-3a2-2a=f(1)≤f(x)≤f(0)=-2a,
结合条件,可以得到1-3a2-2a≤-4≤-3≤-2a,
∴1≤a≤
,
∴实数a的取值范围[1,
].
∴f(x1)-f(x2)
=x13-3a2x12-2ax1-(x23-3a2x22-2ax2)
=(x1-x2)(x12+x1x2+x22-3a2)>0,
∴f(x)单调递减.
(Ⅱ)由函数f(x)的值域为:
1-3a2-2a=f(1)≤f(x)≤f(0)=-2a,
结合条件,可以得到1-3a2-2a≤-4≤-3≤-2a,
∴1≤a≤
| 3 |
| 2 |
∴实数a的取值范围[1,
| 3 |
| 2 |
点评:本题重点考查了函数的单调性的定义、性质、函数的值域求解等知识,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
平面直角坐标系中,双曲线方程
-
=1(m,n>0),A,C是双曲线的两焦点,B是双曲线上的点,在△ABC中,|
|=
,则双曲线的离心率为( )
| x2 |
| m2 |
| y2 |
| n2 |
| sinA-sinB |
| sinC |
| 1 |
| 2 |
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |
定义f(x)•g(x)=
,函数F(x)=(x2-1)•(x)-k的图象与x轴有两个不同的交点,则实数k的取值范围是 ( )
|
| A、k≥3或0≤k<1 |
| B、k>3或0<k<1 |
| C、k≤1或k≥3 |
| D、0≤k≤1或k>3 |
空间直角坐标系中A(1,2,3),B(-1,0,5),C(3,0,4),D(4,1,3),则直线AB与CD的位置关系是( )
| A、平行 | B、垂直 |
| C、相交但不垂直 | D、无法确定 |
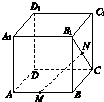 如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点,设
如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点,设| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| MN |
| a |
| b |
| c |
A、x=
| ||||||
B、x=
| ||||||
C、x=
| ||||||
D、x=
|
函数y=x3-3x+k有三个不同的零点,则k的取值范围是( )
| A、(2,+∞) |
| B、(-2,2) |
| C、(-∞,-,2) |
| D、[-2,2] |