题目内容
设与圆(x-1)2+(y-1)2=1相切的直线n:经过两点A(a,0),B(0,b),其中a>2,b>2,O为坐标原点,则△AOB面积的最小值为 .
考点:圆的切线方程
专题:计算题,不等式的解法及应用,直线与圆
分析:根据题意设出直线n的截距式方程,化简得bx+ay-ab=0.由直线n与圆(x-1)2+(y-1)2=1相切,利用点到直线的距离公式列式并化简,得到ab-2a-2b+2=0,再利用基本不等式算出ab≥6+4
.最后根据三角形的面积公式加以计算,可得△AOB面积的最小值为3+2
.
| 2 |
| 2 |
解答:
解:∵直线n经过两点A(a,0)、B(0,b),
∴设直线n的方程为
+
=1,化简得bx+ay-ab=0.
∵直线n与圆(x-1)2+(y-1)2=1相切,
∴圆心(1,1)到直线n的距离等于半径,即
=1,
去分母,平方得(b+a-ab)2=a2+b2,即a2b2+2ab-2a2b-2ab2=0,
化简整理得ab-2a-2b+2=0,
∵a>2且b>2,∴a+b≥2
,(当且仅当a=b时,等号成立)
由此可得ab+2=2(a+b)≥4
,即ab-4
+2≥0,
解之得
≤2-
或
≥2+
.
∵a>2且b>2,∴
>2,可得
≥2+
,ab≥(2+
)2=6+4
,
又∵△AOB的面积S=
|OA|•|OB|=
ab,
∴当且仅当a=b时,△AOB的面积S的最小值S=
(6+4
)=3+2
.
故答案为:3+2

∴设直线n的方程为
| x |
| a |
| y |
| b |
∵直线n与圆(x-1)2+(y-1)2=1相切,
∴圆心(1,1)到直线n的距离等于半径,即
| |b+a-ab| | ||
|
去分母,平方得(b+a-ab)2=a2+b2,即a2b2+2ab-2a2b-2ab2=0,
化简整理得ab-2a-2b+2=0,
∵a>2且b>2,∴a+b≥2
| ab |
由此可得ab+2=2(a+b)≥4
| ab |
| ab |
解之得
| ab |
| 2 |
| ab |
| 2 |
∵a>2且b>2,∴
| ab |
| ab |
| 2 |
| 2 |
| 2 |
又∵△AOB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
∴当且仅当a=b时,△AOB的面积S的最小值S=
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:3+2
| 2 |
点评:本题给出与定圆相切的直线n,求n被坐标轴截得三角形面积的最小值,着重考查了直线的方程、直线与圆的位置关系、点到直线的距离公式、不等式的解法与利用基本不等式求最值等知识,属于中档题.

练习册系列答案
相关题目
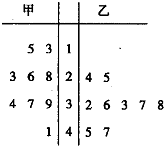 如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为
如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是( )
| A、m∥α,n∥α,则m∥n |
| B、m∥n,m∥α,则n∥α |
| C、m⊥α,m⊥β,则α∥β |
| D、α⊥γ,β⊥γ,则α∥β |
直线
x+y-2=0与圆x2+y2=4相交所得的弦的长为( )
| 3 |
A、2
| ||
B、2
| ||
C、
| ||
D、
|
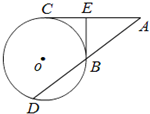 (几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB=
(几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB=