题目内容
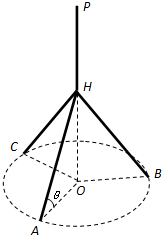如图所示，某人想制造一个支架，它由四根金属杆PH，HA，HB，HC构成，其底端三点A，B，C均匀地固定在半径为3m的圆O上（圆O在地面上），P，H，O三点相异且共线，PO与地面垂直．现要求点P到地面的距离恰为3| 3 |
（1）试将L表示为θ的函数，并注明定义域；
（2）当θ的正弦值是多少时，用料最省？
考点：球的体积和表面积
专题：综合题,导数的综合应用,空间位置关系与距离
分析：（1）利用L=PH+HA+HB+HC，可将L表示为θ的函数，由点P，H重合，确定函数的定义域；
（2）利用导数，确定函数的单调性，即可求出θ的正弦值，用料最省．
（2）利用导数，确定函数的单调性，即可求出θ的正弦值，用料最省．
解答：
解：（1）因PO与地面垂直，且三点A，B，C均匀地固定在半径为3m的圆O上，则△AOH，△BOH，△COH是全等的直角三角形，
又圆O的半径为3，所以OH=3tanθ，AH=BH=CH=
，…（3分）
又PH=3
-3tanθ，所以L=3
-3tanθ+
，…（6分）
若点P，H重合，则tanθ=
，即θ=
，所以θ∈(0，
)，
从而L=3
-3tanθ+
，θ∈(0，
)．…（8分）
（2）由（1）知L=3
-3tanθ+
=3
+3•
，
所以L′=3•
，当L'=0时，sinθ=
，…（12分）
令sinθ0=
，θ0∈(0，
)，当θ∈(θ0，
)时，L'＞0；当θ∈（0，θ0）时，L′＜0；
所以函数L在（0，θ0）上单调递减，在(θ0，
)上单调递增，…（15分）
所以当θ=θ0，即sinθ=
时，L有最小值，此时用料最省．…（16分）
又圆O的半径为3，所以OH=3tanθ，AH=BH=CH=
| 3 |
| cosθ |
又PH=3
| 3 |
| 3 |
| 9 |
| cosθ |
若点P，H重合，则tanθ=
| 3 |
| π |
| 3 |
| π |
| 3 |
从而L=3
| 3 |
| 9 |
| cosθ |
| π |
| 3 |
（2）由（1）知L=3
| 3 |
| 9 |
| cosθ |
| 3 |
| 3-sinθ |
| cosθ |
所以L′=3•
| 3sinθ-1 |
| cos2θ |
| 1 |
| 3 |
令sinθ0=
| 1 |
| 3 |
| π |
| 3 |
| π |
| 3 |
所以函数L在（0，θ0）上单调递减，在(θ0，
| π |
| 3 |
所以当θ=θ0，即sinθ=
| 1 |
| 3 |
点评：本题主要考查了空间想象能力，实际应用能力和建模能力，以及利用导数求函数的最值等有关知识，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
已知三棱锥A-BCD中，侧棱长和底面边长均相等，E为侧棱AB的中点，求证：