题目内容
已知M、N分别是△ADB和△ADC的重心，点A不在平面α内，B、D、C均在平面α内，求证：MN∥α
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：首先根据题意画出相应的图形，再根据M、N分别是△ADB和△ADC的重心，得到MN∥PQ，继而问题得证．
解答：
证明：如图所示，连接AM．AN，FE分别交BD，CD于点P，Q，
则P，Q分别是BD，CD的中点，连接PQ
∵M、N分别是△ADB和△ADC的重心，
∴MN∥PQ，
又PQ?平面BCD，MN?平面BCD，
∴MN∥平面BCD，
B、D、C均在平面α内
∴MN∥α．
证明：如图所示，连接AM．AN，FE分别交BD，CD于点P，Q，则P，Q分别是BD，CD的中点，连接PQ
∵M、N分别是△ADB和△ADC的重心，
∴MN∥PQ，
又PQ?平面BCD，MN?平面BCD，
∴MN∥平面BCD，
B、D、C均在平面α内
∴MN∥α．
点评：本题考查三角形的重心性质，以及线面平行的判定定理，属于中档题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知复数z=i（2+i），则它的共轭复数在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知命题p：“?x∈R，?m∈R，使4x+2x•m+1=0”．若命题p为真命题，则实数m的取值范围是（ ）
| A、（-∞，-2] |
| B、[2，+∞） |
| C、（-∞，-2） |
| D、（2，+∞） |
有一个正三棱柱锤A-BCD零件，P是侧面ACD上一点，在面ACD上过点P画一条与棱AB垂直的线段，怎样画法？并说明理由．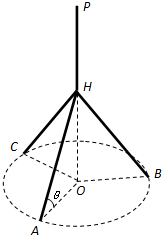
如图所示，某人想制造一个支架，它由四根金属杆PH，HA，HB，HC构成，其底端三点A，B，C均匀地固定在半径为3m的圆O上（圆O在地面上），P，H，O三点相异且共线，PO与地面垂直．现要求点P到地面的距离恰为3