题目内容
若f(log
x)=4x+2,则f(2)的值为 .
| 1 |
| 2 |
考点:函数的值
专题:函数的性质及应用
分析:设log
x=t,则x=(
)t,由此得到f(t)=4(
)t+2,从而能求出f(2)的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:设log
x=t,则x=(
)t,
∵f(log
x)=4x+2,∴f(t)=4(
)t+2,
∴f(2)=4×(
)2+2=3.
故答案为:3.
| 1 |
| 2 |
| 1 |
| 2 |
∵f(log
| 1 |
| 2 |
| 1 |
| 2 |
∴f(2)=4×(
| 1 |
| 2 |
故答案为:3.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意换元法的合理运用.

练习册系列答案
相关题目
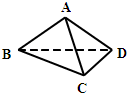 如图,四面体A-BCD中,AB=AD=CD=1,BD=
如图,四面体A-BCD中,AB=AD=CD=1,BD=| 2 |
A、
| ||||
| B、3π | ||||
C、
| ||||
| D、2π |
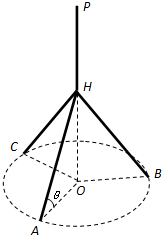 如图所示,某人想制造一个支架,它由四根金属杆PH,HA,HB,HC构成,其底端三点A,B,C均匀地固定在半径为3m的圆O上(圆O在地面上),P,H,O三点相异且共线,PO与地面垂直.现要求点P到地面的距离恰为3
如图所示,某人想制造一个支架,它由四根金属杆PH,HA,HB,HC构成,其底端三点A,B,C均匀地固定在半径为3m的圆O上(圆O在地面上),P,H,O三点相异且共线,PO与地面垂直.现要求点P到地面的距离恰为3