题目内容
设某地区O型血的人数占总人口数的比为
,现从中随机抽取3人.
(1)求3人中恰有2人为O型血的概率;
(2)记O型血的人数为ξ,求ξ的概率分布与数学期望.
| 1 |
| 2 |
(1)求3人中恰有2人为O型血的概率;
(2)记O型血的人数为ξ,求ξ的概率分布与数学期望.
考点:离散型随机变量的期望与方差,n次独立重复试验中恰好发生k次的概率
专题:概率与统计
分析:(1)随机抽取一人,是O型血的概率为
,由此能求出3人中有2人为O型血的概率.
(2)ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的概率分布与数学期望.
| 1 |
| 2 |
(2)ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的概率分布与数学期望.
解答:
(本小题满分14分)
(理)解:(1)由题意,随机抽取一人,是O型血的概率为
,…(2分)
∴3人中有2人为O型血的概率为P=
(
)3=
.…(6分)
(2)ξ的可能取值为0,1,2,3,…(8分)
P(ξ=0)=
(
)3=
,
P(ξ=1)=
(
)3=
,
P(ξ=2)=
(
)3=
,
P(ξ=3)=
(
)3=
,…(12分)
∴ξ的分布鞋列为:
∴Eξ=1×
+2×
+3×
=
.…(14分)
(理)解:(1)由题意,随机抽取一人,是O型血的概率为
| 1 |
| 2 |
∴3人中有2人为O型血的概率为P=
| C | 2 3 |
| 1 |
| 2 |
| 3 |
| 8 |
(2)ξ的可能取值为0,1,2,3,…(8分)
P(ξ=0)=
| C | 0 3 |
| 1 |
| 2 |
| 1 |
| 8 |
P(ξ=1)=
| C | 1 3 |
| 1 |
| 2 |
| 3 |
| 8 |
P(ξ=2)=
| C | 2 3 |
| 1 |
| 2 |
| 3 |
| 8 |
P(ξ=3)=
| C | 3 3 |
| 1 |
| 2 |
| 1 |
| 8 |
∴ξ的分布鞋列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 3 |
| 8 |
| 3 |
| 8 |
| 1 |
| 8 |
| 3 |
| 2 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
已知命题p:“?x∈R,?m∈R,使4x+2x•m+1=0”.若命题p为真命题,则实数m的取值范围是( )
| A、(-∞,-2] |
| B、[2,+∞) |
| C、(-∞,-2) |
| D、(2,+∞) |
 有一个正三棱柱锤A-BCD零件,P是侧面ACD上一点,在面ACD上过点P画一条与棱AB垂直的线段,怎样画法?并说明理由.
有一个正三棱柱锤A-BCD零件,P是侧面ACD上一点,在面ACD上过点P画一条与棱AB垂直的线段,怎样画法?并说明理由.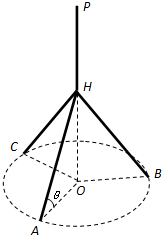 如图所示,某人想制造一个支架,它由四根金属杆PH,HA,HB,HC构成,其底端三点A,B,C均匀地固定在半径为3m的圆O上(圆O在地面上),P,H,O三点相异且共线,PO与地面垂直.现要求点P到地面的距离恰为3
如图所示,某人想制造一个支架,它由四根金属杆PH,HA,HB,HC构成,其底端三点A,B,C均匀地固定在半径为3m的圆O上(圆O在地面上),P,H,O三点相异且共线,PO与地面垂直.现要求点P到地面的距离恰为3