P是双曲线$\frac{x^2}{64}-\frac{y^2}{36}=1$上一点.F1.F2是双曲线的两个焦点.且|PF1|=15.则|PF2|的值是31．题目和参考答案——青夏教育精英家教网——

题目内容

3．P是双曲线$\frac{x^2}{64}-\frac{y^2}{36}=1$上一点，F₁，F₂是双曲线的两个焦点，且|PF₁|=15，则|PF₂|的值是31．

分析求出双曲线的a，b，c，根据|PF₁|=15＜c+a=18，则P在双曲线的左支上，再由双曲线的定义，即可得到所求值．

解答双曲线的a=8，b=6，c=10，
由于|PF₁|=15＜c+a=18，
则P在双曲线的左支上，
由双曲线的定义，可得，
|PF₂|-|PF₁|=2a=16，
则有|PF₂|=16+|PF₁|=16+15=31．
故答案为：31．

点评本题考查双曲线的方程和性质、定义，考查运算能力，属于基础题和易错题

练习册系列答案

期末测试卷系列答案

小学培优总复习系列答案

小学科学探究手册系列答案

小学达标训练系列答案

小学毕业综合复习系列答案

小学毕业特训卷系列答案

小学毕业升学总复习系列答案

小学毕业升学模拟试卷系列答案

打好双基名校名师模拟卷系列答案

归类复习模拟试卷系列答案

相关题目

13．已知F₁（-3，0），F₂（3，0），满足条件|PF₁|-|PF₂|=2m-1的动点P的轨迹是双曲线的一支．下列数据：①2；②-1；③4；④-3；⑤$\frac{1}{2}$，则m可以是（　　）

14．已知抛物线C：y²=2px的焦点坐标为F（2，0），则p=4；若已知点A（6，3），且点M在抛物线C上，则|MA|+|MF|的最小值为8．

11．已知奇函数f（x），且f（a）=11，则f（-a）=-11．

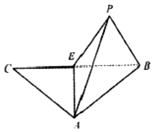等腰△ABC，E为底边BC的中点，沿AE折叠，如图，将C折到点P的位置，使二面角P-AE-C的大小为120°，设点P在面ABE上的射影为H．
（I）证明：点H为BE的中点；
（II）若AB=AC=2$\sqrt{2}$，AB⊥AC，求直线BE与平面ABP所成角的正切值．

8．已知全集U=R，集合A={x|x²-x-2≥0}，B={x|log₃x＜1，则（∁_UA）∩B=（　　）

15．已知函数$f（x）=2msinx-2{cos^2}x+\frac{m^2}{2}-4m+3$，且函数f（x）的最小值为-7，求实数m的值．

12．双曲线$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{4}$=1的焦距为6，则m的值是（　　）

13．在△ABC中，∠A，∠B，∠C所对的边分别是a，b，c．当钝角△ABC的三边a，b，c是三个连续整数时，则△ABC外接圆的半径为$\frac{{8\sqrt{15}}}{15}$．