题目内容
8.已知tanθ=4,则$\frac{sinθ+cosθ}{17sinθ}+\frac{{si{n^2}θ}}{4}$的值为( )| A. | $\frac{14}{68}$ | B. | $\frac{21}{68}$ | C. | $\frac{68}{14}$ | D. | $\frac{68}{21}$ |
分析 利用同角三角函数间的基本关系化简,把tanθ的值代入计算即可求出值.
解答 解:$\frac{sinθ+cosθ}{17sinθ}+\frac{{si{n^2}θ}}{4}$=$\frac{tanθ+1}{17tanθ}+\frac{si{n}^{2}θ}{4(si{n}^{2}θ+co{s}^{2}θ)}$
=$\frac{tanθ+1}{17tanθ}+\frac{ta{n}^{2}θ}{4(ta{n}^{2}θ+1)}$=$\frac{4+1}{68}+\frac{16}{68}=\frac{21}{68}$.
故选:B.
点评 本题考查了同角三角函数间基本关系的运用,熟练掌握基本关系是解本题的关键,是基础题.

练习册系列答案
相关题目
3.已知函数f(x)=2x+2,则f(2)的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
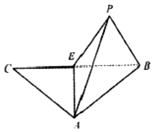 等腰△ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使二面角P-AE-C的大小为120°,设点P在面ABE上的射影为H.
等腰△ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使二面角P-AE-C的大小为120°,设点P在面ABE上的射影为H.