题目内容
9.已知函数$f(x)=sin(ωx+\frac{π}{6})+ω(ω>0)$的部分图象如图所示,则下列选项判断错误的是( )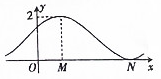
| A. | |MN|=π | B. | $f(\frac{7π}{3})=2$ | C. | $f(x)+f(-x-\frac{π}{3})=1$ | D. | $f(\frac{π}{3}-x)=f(\frac{π}{3}+x)$ |
分析 根据函数的部分图象知ω=1,写出f(x)的解析式,再对选项中的命题进行分析、判断正误.
解答 解:根据函数$f(x)=sin(ωx+\frac{π}{6})+ω(ω>0)$的部分图象知,
ω=1,∴f(x)=sin(x+$\frac{π}{6}$)+1;
∴|MN|=$\frac{1}{2}$T=π,A正确;
f($\frac{7π}{3}$)=sin($\frac{7π}{3}$+$\frac{π}{6}$)+1=2,B正确;
f(x)+f(-x-$\frac{π}{3}$)=sin(x+$\frac{π}{6}$)+1+sin(-x-$\frac{π}{3}$+$\frac{π}{6}$)+1
=sinxcos$\frac{π}{6}$+cosxsin$\frac{π}{6}$-sinxcos$\frac{π}{3}$-cosxsin$\frac{π}{3}$+2
=$\frac{\sqrt{3}-1}{2}$(sinx-cosx)+2≠1,C错误;
x=$\frac{π}{3}$是f(x)=sin(x+$\frac{π}{6}$)图象的一条对称轴,
∴f($\frac{π}{3}$-x)=f($\frac{π}{3}$+x),D正确.
故选:C.
点评 本题考查了正弦函数的图象与性质的应用问题,是基础题.

练习册系列答案
相关题目
13.已知a=log${\;}_{\frac{1}{5}}$$\frac{1}{3}$,b=log35,c=log5(cos$\frac{1}{5}$π),则( )
| A. | b<a<c | B. | a<b<c | C. | c<b<a | D. | c<a<b |
1.已知偶函数f(x)对任意x∈R都有f(x)=f(x-4),且f(x)在区间[-2,0]上有f(x)=$\left\{\begin{array}{l}{-{x}^{2}+\frac{3}{2}x+5,-1≤x≤0}\\{{2}^{-x}+{2}^{x},-2≤x<-1}\end{array}\right.$,若方程f(x)=($\frac{1}{2}$)|x|+b恰好有4个不等的实数根,则实数b的取值范围是( )
| A. | (0,2) | B. | (2,$\frac{33}{8}$) | C. | (2,$\frac{19}{8}$) | D. | ($\frac{19}{8}$,$\frac{33}{8}$) |
19.“?p是真”是“p∨q为假”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图所示在四棱锥A-BCDM中,BD⊥平面ABC,AC=BC,N是棱AB的中点.
如图所示在四棱锥A-BCDM中,BD⊥平面ABC,AC=BC,N是棱AB的中点.