已知$f=2x+1.x∈[{-\frac{π}{2}.\frac{π}{2}}]$.则f=21-7π．题目和参考答案——青夏教育精英家教网—

题目内容

15．已知$f（{sinx}）=2x+1，x∈[{-\frac{π}{2}，\frac{π}{2}}]$，则f（cos10）=21-7π．

分析 f（cos10）=f[sin（10-$\frac{7π}{2}$）]，由此能求出结果．

解答解：∵$f（{sinx}）=2x+1，x∈[{-\frac{π}{2}，\frac{π}{2}}]$，
∴f（cos10）=f[sin（10-$\frac{7π}{2}$）]=2（10-$\frac{7π}{2}$）+1=21-7π．
故答案为：21-7π．

点评本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

练习册系列答案

超能学典名牌中学期末突破一卷通系列答案

	A．	必要不充分条件		B．	充分不必要条件
	C．	充分必要条件		D．	既不充分也不必要条件

6．已知函数f（x）=ln（1+ax）-$\frac{2x}{x+2}$（a＞0）
（1）当a=$\frac{1}{2}$ 时，求f（x）的极值；
（2）若a∈（$\frac{1}{2}$，1）时f（x）存在两个极值点x₁，x₂，试比较f（x₁）+f（x₂）与f（0）的大小．

3．已知f（sin x）=x且x∈[0，$\frac{π}{2}$]，则f（$\frac{1}{2}$）=$\frac{π}{6}$．

10．已知集合U=R，A={x|（x-2）（x+1）≤0}，B={x|0≤x＜3}，则∁_U（A∪B）=（　　）

20．

如图，在直角梯形ABCD中，AB⊥AD，AB∥DC，AB=2，AD=DC=1，图中圆弧所在圆的圆心为点C，半径为$\frac{1}{2}$，且点P在图中阴影部分（包括边界）运动．若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$，其中x，y∈R，则4x-y的最大值为（　　）

A．

$3-\frac{{\sqrt{2}}}{4}$

B．

$3+\frac{{\sqrt{5}}}{2}$

C．

D．

$3+\;\frac{{\sqrt{17}}}{2}$

7．已知函数f（x）是（-∞，+∞）上的增函数，a，b∈R，命题：若a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）
判断此命题的逆命题是否成立，并用反证法证明你的结论．

9．已知函数$f（x）=sin（ωx+\frac{π}{6}）+ω（ω＞0）$的部分图象如图所示，则下列选项判断错误的是（　　）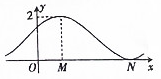

$f（x）+f（-x-\frac{π}{3}）=1$

D．

$f（\frac{π}{3}-x）=f（\frac{π}{3}+x）$

试题分类