题目内容
1.已知偶函数f(x)对任意x∈R都有f(x)=f(x-4),且f(x)在区间[-2,0]上有f(x)=$\left\{\begin{array}{l}{-{x}^{2}+\frac{3}{2}x+5,-1≤x≤0}\\{{2}^{-x}+{2}^{x},-2≤x<-1}\end{array}\right.$,若方程f(x)=($\frac{1}{2}$)|x|+b恰好有4个不等的实数根,则实数b的取值范围是( )| A. | (0,2) | B. | (2,$\frac{33}{8}$) | C. | (2,$\frac{19}{8}$) | D. | ($\frac{19}{8}$,$\frac{33}{8}$) |
分析 作出函数图象,根据函数对称性可得f(x)和y=($\frac{1}{2}$)|x|+b在(0,+∞)上有2个交点,根据图象列出不等式解出b的范围.
解答 解:∵f(x)=f(x-4),∴f(x)的周期为4,
又f(x)是偶函数,作出f(x)和y=($\frac{1}{2}$)|x|+b在(0,+∞)上的函数图象如图所示: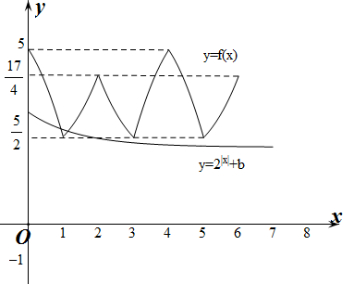
∵y=f(x)与y=($\frac{1}{2}$)|x|+b都是偶函数,且方程f(x)=($\frac{1}{2}$)|x|+b恰好有4个不等的实数根,
∴f(x)和y=($\frac{1}{2}$)|x|+b在(0,+∞)上有2个交点,
∴$\left\{\begin{array}{l}{\frac{1}{2}+b>\frac{5}{2}}\\{\frac{1}{8}+b<\frac{5}{2}}\end{array}\right.$,解得2<b<$\frac{19}{8}$.
故选C.
点评 本题考查了分段函数的图象,函数的周期应用,函数零点与函数图象的关系,属于中档题.

练习册系列答案
相关题目
9.已知函数$f(x)=sin(ωx+\frac{π}{6})+ω(ω>0)$的部分图象如图所示,则下列选项判断错误的是( )

| A. | |MN|=π | B. | $f(\frac{7π}{3})=2$ | C. | $f(x)+f(-x-\frac{π}{3})=1$ | D. | $f(\frac{π}{3}-x)=f(\frac{π}{3}+x)$ |
16.{an}是a1=2,d=2的等差数列,其前n项和公式为( )
| A. | Sn=n2-n | B. | Sn=n2-2n | C. | Sn=n2+n | D. | Sn=n2+2n |
6.已知a,b,c分别是△ABC中角A,B,C的对边,G是△ABC的三条边上中线的交点,若$\overrightarrow{GA}+(a+b)\overrightarrow{GB}+2c\overrightarrow{GC}$=$\overrightarrow 0$,且$\frac{1}{a}+\frac{4}{b}$≥m+c恒成立,则实数m的取值范围为( )
| A. | $(-∞,\frac{17}{2}]$ | B. | $(-∞,\frac{13}{2}]$ | C. | $[\frac{13}{2},+∞)$ | D. | $[\frac{17}{2},+∞)$ |
10.若集合A={(m,n)|(m+1)+(m+2)+…+(m+n)=102015,m∈N,n∈N*},则集合A中的元素个数是( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |