题目内容
16.圆(x-1)2+(y-1)2=1上的点到直线x-y=2的距离的最大值是1+$\sqrt{2}$.分析 明确圆心和半径,再求得圆心(1,1)到直线x-y=2的距离,最大值则在此基础上加上半径长即可.
解答 解:圆(x-1)2+(y-1)2=1的圆心为(1,1),
圆心到直线x-y=2的距离为$\frac{|1-1-2|}{\sqrt{1+1}}$=$\sqrt{2}$,
圆心到直线的距离加上半径就是圆上的点到直线的最大距离,即最大距离为1+$\sqrt{2}$.
故答案为1+$\sqrt{2}$.
点评 本题主要考查直线与圆的位置关系,当考查圆上的点到直线的距离问题,基本思路是:先求出圆心到直线的距离,最大值时,再加上半径,最小值时,再减去半径.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
4.函数y=cos2x的导数是( )
| A. | -sin2x | B. | sin2x | C. | -2sin2x | D. | 2sin2x |
11.欧拉(LeonhardEuler,国籍瑞士)是科学史上最多产的一位杰出的数学家,他发明的公式eix=cosx+isinx(i为虚数单位),将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,这个公式在复变函数理论中占有非常重要的地位,被誉为“数学中的天桥”.根据此公式可知,表示的复数${e^{\frac{2π}{3}i}}$在复平面内位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.已知函数$f(x)=sin(ωx+\frac{π}{6})+ω(ω>0)$的部分图象如图所示,则下列选项判断错误的是( )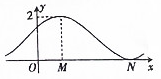

| A. | |MN|=π | B. | $f(\frac{7π}{3})=2$ | C. | $f(x)+f(-x-\frac{π}{3})=1$ | D. | $f(\frac{π}{3}-x)=f(\frac{π}{3}+x)$ |
10.若集合A={(m,n)|(m+1)+(m+2)+…+(m+n)=102015,m∈N,n∈N*},则集合A中的元素个数是( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |