题目内容
13.已知a=log${\;}_{\frac{1}{5}}$$\frac{1}{3}$,b=log35,c=log5(cos$\frac{1}{5}$π),则( )| A. | b<a<c | B. | a<b<c | C. | c<b<a | D. | c<a<b |
分析 利用对数函数的单调性直接求解.
解答 解:∵0=$lo{g}_{\frac{1}{5}}1$<a=log${\;}_{\frac{1}{5}}$$\frac{1}{3}$<$lo{g}_{\frac{1}{5}}\frac{1}{5}$=1,
b=log35>log33=1,
c=log5(cos$\frac{1}{5}$π)<log51=0,
∴c<a<b.
故选:D.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意对数函数的单调性的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.函数y=cos2x的导数是( )
| A. | -sin2x | B. | sin2x | C. | -2sin2x | D. | 2sin2x |
9.已知函数$f(x)=sin(ωx+\frac{π}{6})+ω(ω>0)$的部分图象如图所示,则下列选项判断错误的是( )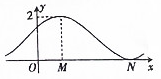

| A. | |MN|=π | B. | $f(\frac{7π}{3})=2$ | C. | $f(x)+f(-x-\frac{π}{3})=1$ | D. | $f(\frac{π}{3}-x)=f(\frac{π}{3}+x)$ |
6.已知a,b,c分别是△ABC中角A,B,C的对边,G是△ABC的三条边上中线的交点,若$\overrightarrow{GA}+(a+b)\overrightarrow{GB}+2c\overrightarrow{GC}$=$\overrightarrow 0$,且$\frac{1}{a}+\frac{4}{b}$≥m+c恒成立,则实数m的取值范围为( )
| A. | $(-∞,\frac{17}{2}]$ | B. | $(-∞,\frac{13}{2}]$ | C. | $[\frac{13}{2},+∞)$ | D. | $[\frac{17}{2},+∞)$ |
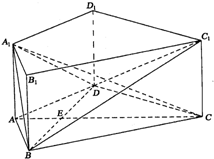 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2$\sqrt{3}$,AA1=$\sqrt{3}$,AD⊥DC,AC⊥BD,垂足为E,
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2$\sqrt{3}$,AA1=$\sqrt{3}$,AD⊥DC,AC⊥BD,垂足为E,