题目内容
14.三棱锥M-ABC的三侧棱两两垂直,底面ABC内一点N到三个侧面的距离分别为$2\sqrt{2},4,5$,则经过点M和N的所有球中,体积最小的球的表面积为49π.分析 根据题意,点Q到三个侧面的垂线与侧棱PA、PB、PC围成一个棱长为2$\sqrt{2}$、4、5的长方体,分析可知以PQ为直径的球是它的外接球,此时过点P和Q的所有球中,表面积最小的球,即可求解
解答 解:根据题意:点Q到三个侧面的垂线与侧棱PA、PB、PC围成一个棱长为2$\sqrt{2}$、4、5的长方体,内部图形如图.
则其外接球的直径即为PQ且为长方体的体对角线,过点P和Q的所有球中,此时外接球的表面积最小,
此时,长方体对角线即为球的直径,∴2R=$\sqrt{{4}^{2}+{5}^{2}+(2\sqrt{2})^{2}}=7$、
由球的表面积公式得:S=4πR2=49π,
故答案为:49π.
点评 本题主要考查空间几何体的构造和组合体的基本关系.判断长方体的对角线是过P和Q的所有球中,最小的球是解题的关键.属于中档题

练习册系列答案
相关题目
20. 如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$,其中x,y∈R,则4x-y的最大值为( )
如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$,其中x,y∈R,则4x-y的最大值为( )
 如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$,其中x,y∈R,则4x-y的最大值为( )
如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{BC}$,其中x,y∈R,则4x-y的最大值为( )| A. | $3-\frac{{\sqrt{2}}}{4}$ | B. | $3+\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | $3+\;\frac{{\sqrt{17}}}{2}$ |
9.已知函数$f(x)=sin(ωx+\frac{π}{6})+ω(ω>0)$的部分图象如图所示,则下列选项判断错误的是( )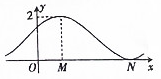

| A. | |MN|=π | B. | $f(\frac{7π}{3})=2$ | C. | $f(x)+f(-x-\frac{π}{3})=1$ | D. | $f(\frac{π}{3}-x)=f(\frac{π}{3}+x)$ |
19.已知A,B,C不共线,对空间任意一点O,若$\overrightarrow{OP}$=$\frac{1}{2}$$\overrightarrow{OA}$+($\frac{1}{4}$-λ)$\overrightarrow{OB}$+(λ+$\frac{1}{4}$)$\overrightarrow{OC}$成立,则“λ=1”是“P,A,B,C四点共面”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
6.已知a,b,c分别是△ABC中角A,B,C的对边,G是△ABC的三条边上中线的交点,若$\overrightarrow{GA}+(a+b)\overrightarrow{GB}+2c\overrightarrow{GC}$=$\overrightarrow 0$,且$\frac{1}{a}+\frac{4}{b}$≥m+c恒成立,则实数m的取值范围为( )
| A. | $(-∞,\frac{17}{2}]$ | B. | $(-∞,\frac{13}{2}]$ | C. | $[\frac{13}{2},+∞)$ | D. | $[\frac{17}{2},+∞)$ |
4.已知集合M={x|y=ln(x2-3x-4)},N={y|y=2x-1},则M∩N等于( )
| A. | {x|x>4} | B. | {x|x>0} | C. | {x|x<-1} | D. | {x|x>4或x<-1} |
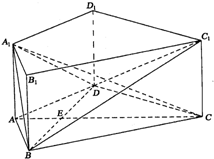 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2$\sqrt{3}$,AA1=$\sqrt{3}$,AD⊥DC,AC⊥BD,垂足为E,
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2$\sqrt{3}$,AA1=$\sqrt{3}$,AD⊥DC,AC⊥BD,垂足为E,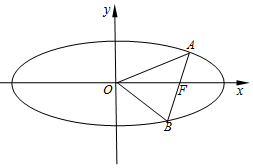 如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为$\frac{{4\sqrt{3}}}{3}$.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2,过右焦点F的直线l交椭圆于A、B两点,当l与x轴垂直时,AB长为$\frac{{4\sqrt{3}}}{3}$.