题目内容
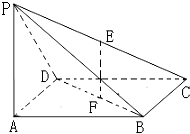 如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
| ||
| 2 |
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)求空间几何体BCDP的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)利用线面平行的判定定理:连接AC,只需证明EF∥PA,利用中位线定理即可得证;
(Ⅱ)设AD的中点为G,连接PG,证明PG⊥底面ABCD,可求空间几何体BCDP的体积.
(Ⅱ)设AD的中点为G,连接PG,证明PG⊥底面ABCD,可求空间几何体BCDP的体积.
解答:
(Ⅰ)证明:连接AC,
∵底面ABCD是边长为a的正方形,并且F是BD的中点,
∴F是AC的中点,-----------------------------------------------------------(2分)
在△PAC中,F是AC的中点,E是PC的中点,
∴EF∥PA,---------------------------------------------------------------------------(4分)
∵EF?平面PAD,PA?平面PAD,
∴EF∥平面PAD.--------------------------------(6分)
(Ⅱ)解:∵侧面PAD⊥底面ABCD,交线是AD,
在△PAD中,PA=PD=
AD
∴△PAD是等腰直角三角形,
设AD的中点为G,连接PG,则PG⊥AD,且PG=
a-----------------------------(6分)
∴PG⊥底面ABCD,
∴空间几何体BCDP的体积是:VBCDP=VP-BCD=
×S△BCD×PG=
a3.---------------(12分)
∵底面ABCD是边长为a的正方形,并且F是BD的中点,
∴F是AC的中点,-----------------------------------------------------------(2分)
在△PAC中,F是AC的中点,E是PC的中点,
∴EF∥PA,---------------------------------------------------------------------------(4分)
∵EF?平面PAD,PA?平面PAD,
∴EF∥平面PAD.--------------------------------(6分)
(Ⅱ)解:∵侧面PAD⊥底面ABCD,交线是AD,
在△PAD中,PA=PD=
| ||
| 2 |
∴△PAD是等腰直角三角形,
设AD的中点为G,连接PG,则PG⊥AD,且PG=
| 1 |
| 2 |
∴PG⊥底面ABCD,
∴空间几何体BCDP的体积是:VBCDP=VP-BCD=
| 1 |
| 3 |
| 1 |
| 12 |
点评:本题考查直线与平面平行的证明,考查空间几何体BCDP的体积,解题时要合理地化空间问题为平面问题,属于中档题.

练习册系列答案
相关题目
由大于-8小于20的奇数所组成的集合( )
| A、{x∈Z|-8<x<20} |
| B、{x|-8<x<20,x=2k+1,k∈N} |
| C、{x|-8<x<20} |
| D、{x|-8<x<20,x=2k+1,k∈Z} |
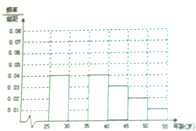 某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.
某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.