题目内容
函数y=tanωx的最小正周期为
,则正实数ω的值为 .
| π |
| 2 |
考点:三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:由条件利用函数y=Atan(ωx+φ)的周期为
,可得结论.
| π |
| ω |
解答:
解:∵函数y=tanωx的最小正周期为
,∴
=
,求得正实数ω=2,
故答案为:2.
| π |
| 2 |
| π |
| ω |
| π |
| 2 |
故答案为:2.
点评:本题主要考查函数y=Atan(ωx+φ)的周期性,利用了函数y=Atan(ωx+φ)的周期为
,属于基础题.
| π |
| ω |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=sin2x的导数是( )
| A、2sinx |
| B、2cosx |
| C、2sin2x |
| D、sin2x |
函数f(x)=cos2x+2sinx的最大值与最小值的和是( )
| A、-2 | ||
| B、0 | ||
C、-
| ||
D、-
|
下列函数中为奇函数的是( )
| A、f(x)=x3 |
| B、f(x)=x2+1 |
| C、f(x)=cosx |
| D、f(x)=lgx |
由大于-8小于20的奇数所组成的集合( )
| A、{x∈Z|-8<x<20} |
| B、{x|-8<x<20,x=2k+1,k∈N} |
| C、{x|-8<x<20} |
| D、{x|-8<x<20,x=2k+1,k∈Z} |
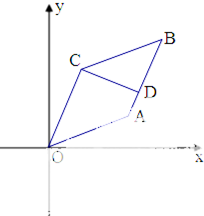 如图,在平行四边形OABC中,已知点A(3,1),C(1,3).
如图,在平行四边形OABC中,已知点A(3,1),C(1,3).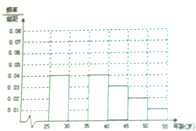 某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.
某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.