题目内容
集合{(x,y)
}⊆{(x,y)|y=3x+b},则b= .
|
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:由题意解方程组
,得集合{(x,y)
}={(0,2)},从而可知(0,2)满足y=3x+b,从而解出b.
|
|
解答:
解:由
解得,x=0,y=2;
则集合{(x,y)
}={(0,2)},
∵{(x,y)
}⊆{(x,y)|y=3x+b},
∴(0,2)满足y=3x+b,代入解得,
b=2.
故答案为:2.
|
则集合{(x,y)
|
∵{(x,y)
|
∴(0,2)满足y=3x+b,代入解得,
b=2.
故答案为:2.
点评:本题考查了方程组的解法即集合的化简与集合包含关系的应用,属于基础题.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
| ∫ | 2 1 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x3 |
A、ln 2+
| ||
B、ln 2-
| ||
C、ln 2-
| ||
D、ln 2-
|
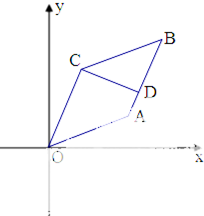 如图,在平行四边形OABC中,已知点A(3,1),C(1,3).
如图,在平行四边形OABC中,已知点A(3,1),C(1,3).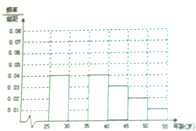 某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.
某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.