题目内容
已知函数f（x）=
x3+
ax2+bx+c的两个极值点分别为x1和x2，有f（x1）=x2，f（x2）=x1，其中x1≠x2，则函数g（x）=f2（x）+af（x）+b的零点个数为 ．
| 1 |
| 3 |
| 1 |
| 2 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：求导数f′（x），由题意知x1，x2是方程x2+ax+b=0的两根，从而关于f（x）的方程（f（x））2+af（x）+b=0有两个根，作出草图，由图象可得答案．
解答：
解：∵f（x）=
x3+
ax2+bx+c有极值点x1，x2，
∴f′（x）=x2+ax+b，
且x1，x2是方程x2+ax+b=0的两根，
不妨设x2＞x1，
由（f（x））2+af（x）+b=0，
则有两个f（x）使等式成立，
x2=f（x1），x2＞x1=f（x2），
如图所示：
有4个交点，
故答案为：4．
| 1 |
| 3 |
| 1 |
| 2 |
∴f′（x）=x2+ax+b，
且x1，x2是方程x2+ax+b=0的两根，
不妨设x2＞x1，
由（f（x））2+af（x）+b=0，
则有两个f（x）使等式成立，
x2=f（x1），x2＞x1=f（x2），
如图所示：
有4个交点，
故答案为：4．
点评：本题主要考查函数零点的概念、函数的极值和函数的导数之间的关系，利用是数形结合是解决本题的关键．
练习册系列答案
相关题目
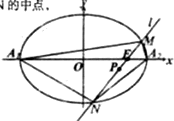已知椭圆C：