题目内容

若关于x的方程
3
sinx+cosx=k在区间[0，
π
2
]上有两个不同的实数解，则实数k的取值范围为
 
．
考点：两角和与差的正弦函数
专题：三角函数的图像与性质
分析：方程
3
sinx+cosx=k在区间[0，
π
2
]上有两个不同的实数解，可以将方程转化为：sin（x+
π
6
）=
k
2
，画出这两个函数的图象，利用数形结合的方法进行求解；
解答： 解：∵方程
3
sinx+cosx=k，
∴2sin（x+
π
6
）=k，即sinx（x+
π
6
）=
k
2
，
可以令f（x）=sinx（x+
π
6
），h（x）=
k
2
，
∵方程
3
sinx+cosx=k在区间[0，
π
2
]上有两个不同的实数解
∴函数f（x）和h（x）的图象有两个交点，
如下图：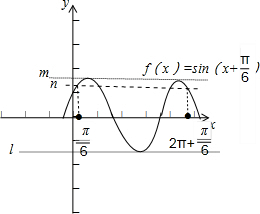
∴
π
6
≤x+
π
6
≤
2π
3

∴h（x）=
k
2
，要使y=f（x）与y=h（x）有两个交点，
∴y=h（x）在直线m和直线n之间，有两个交点，
∴
3
2
≤
k
2
＜1，
∴
3
≤k＜2．
故答案为：[
3
，2）．
点评：本题主要考查函数的零点及函数的零点存在性定理，函数的零点的研究就可转化为相应方程根的问题，数形结合的思想得到了很好的体现．
练习册系列答案
相关题目
已知圆C1：（x+1）2+y2=1和圆C2：（x-4）2+y2=4．
（1）过圆心C1作倾斜角为θ的直线l交圆C2于A，B两点，且A为C1B的中点，求sinθ；
（2）过点P（m，1）引圆C2的两条割线l1和l2，直线l1和l2被圆C2截得的弦的中点分别为M，N．试问过点P，M，N，C2的圆是否过定点（异于点C2）？若过定点，求出该定点；若不过定点，说明理由；
（3）过圆C2上任一点Q（x0，y0）作圆C1的两条切线，设两切线分别与y轴交于点S和T，求线段ST长度的取值范围．
设函数f（x）=
e2x
x-1

（1）求函数的单调区间；
（2）若当x≥2时，f′（x）≥af（x）恒成立，求实数a的取值范围．
已知函数f（x）=x4+ax3+bx+c（a，b，c∈R），g（x）=f′（x）且g（0）=g（1）．
（Ⅰ）求实数a的值；
（Ⅱ）若任意x1、x2∈[0，1]且x2＞x1，求证：|g（x2）-g（x1）|＜8|x2-x1|；
（Ⅲ）当b≤
16
3
9
时，请判断曲线f（x）的所有切线中，斜率λ为正数时切线的条数，并说明理由．
设函数f（x）满足f（x）=f（3x），且当x∈[1，3）时，f（x）=lnx．若在区间[1，9）内，存在3个不同的实数x1，x2，x3，使得
f(x1)
x1
=
f(x2)
x2
=
f(x3)
x3
=t，则实数t的取值范围为
 
．
将三个半径为3的球两两相切地放在水平桌面上，若在这三个球的上方放置一个半径为1的小球，使得这四个球两两相切，则该小球的球心到桌面的距离为
 
．
双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0），双曲线l的渐近线与抛物线y2=8x的准线的一个交点纵坐标为-1，则双曲线的离心率为
 
．
已知函数f（x）=
1
3
x3+
1
2
ax2+bx+c的两个极值点分别为x1和x2，有f（x1）=x2，f（x2）=x1，其中x1≠x2，则函数g（x）=f2（x）+af（x）+b的零点个数为
 
．
若等比数列{an}的前n项和Sn=2•3n-2+a，等差数列{bn}的前n项和Tn=2n2-n+b，则a+b=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网