题目内容
某校组织数学竞赛，学生成绩ξ-N（100，σ2），P（ξ≥120）=a，P（80＜ξ≤100）=b，则a+b= ．
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：由于ξ-N（100，σ2），即曲线关于直线x=100对称，根据概率分布的对称性即可求出a+b的值．
解答：
解：学生成绩ξ-N（100，σ2），即曲线关于直线x=100对称，
由于P（80＜ξ≤100）=b，所以P（100≤ξ＜120）=b，
又P（ξ≥120）=a，所以a+b=P（100≤ξ＜120）+P（ξ≥120）=P（ξ≥100）=0.5．
故答案为：0.5．
由于P（80＜ξ≤100）=b，所以P（100≤ξ＜120）=b，
又P（ξ≥120）=a，所以a+b=P（100≤ξ＜120）+P（ξ≥120）=P（ξ≥100）=0.5．
故答案为：0.5．
点评：本题主要考查了连续型随机变量的概率分布：正态分布的意义和应用，正态分布曲线的对称性，转化化归的思想方法，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
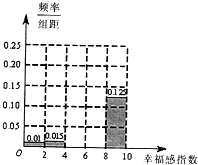“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时，给出的区间内的一个数，该数越接近10表示越满意，为了解某大城市市民的幸福感，随机对该城市的男、女各500人市民进行了调查，调查数据如下表所示：某几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|