Question

若点P在平面区域

x-y-2≤0 x+2y-5≥0 y-2≤0

上，则u=

(x+y)2

xy

的取值范围为

 

．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：画出约束条件表示的可行域，求出

y

x

的范围，然后求解u=

(x+y)2

xy

的取值范围

解答： 解：u=

(x+y)2

xy

=

y

x

+

x

y

+2，
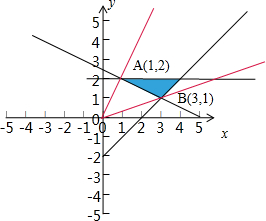
由题意可知约束条件

x-y-2≤0 x+2y-5≥0 y-2≤0

表示的可行域如图：

y

x

表示可行域内的点与坐标原点连线的斜率，显然

y

x

∈[

1

3

，2]，
u=

(x+y)2

xy

=

y

x

+

x

y

+2≥2

y x • x y

+2=4，
当且仅当x=y=1时，不等式成立，
当

y

x

=

1

3

时u=

1

3

+3+2=

16

3

，
当

y

x

=2时，u=2+

1

2

+2=

9

2

＜

16

3

．
∴u=

(x+y)2

xy

的取值范围为：[4，

16

3

]．
故答案为：[4，

16

3

]．

点评：本题考查线性规划的应用，基本不等式的应用，正确分析与判断所求表达式以及作出可行域是解题的关键．