题目内容
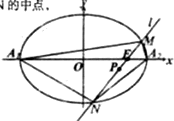已知椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
（1）求椭圆C的方程；
（2）若
| A1N |
| MA2 |
| A1M |
| NA2 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：（1）将直线方程代入椭圆方程并整理，利用韦达定理求得点P的坐标，再根据OP=
=-
，可得3a2=4b2．在直线l的方程中令y=0得，x=1，可得右焦点F（1，0），c=1．求得a2和b2的值，可得椭圆方程．
（2）联立方程组：
，消元并整理，利用韦达定理，由
•
+
•
=12求得k的值．
| yp |
| xp |
| 3 |
| 4 |
（2）联立方程组：
|
| A1N |
| MA2 |
| A1M |
| NA2 |
解答：
解：（1）将直线方程y=x-1代入椭圆方程并整理得：（a2+b2）x2-2a2x+a2-a2b2=0，
设M（x1，y1），N（x2，y2），则x1，x2是方程的两个根，
由韦达定理得：x1+x2=
，x1x2 =
，
y1+y2=x1+x2-2=
，∴xP =
=
，yP=
=
，
∴kOP =
=-
=-
，∴3a2=4b2．
在直线l的方程中令y=0得，x=1，∴F（1，0），∴c=1．
解得：a2=4，b2=3，∴椭圆方程为：
+
=1．
（2）联立方程组：
，消元并整理得：（4k2+3）x2-8k2x+4k2-12=0．
∵△=（-8k2）2-4（4k2+3）（ 4k2-12）=144（k2+1）＞0，
x1+x2=
，x1x2=
，
∴y1+y2=k（x1+x2-2）=
，y1y2=
．
再由 A1（-2，0），A2（2，0），M（x1，y1），N（x2，y2），
=（x2+2，y2），
=（2-x1，-y1），
=（x1+2，y1），
=（2-x2，-y2），
由
•
+
•
=12得：（x2+2）（2-x1）-y1y2+（ x1+2）（ 2-x2）-y1y2=12，
花间得-2x1x2-2y1y2+8=12，∴x1x2+y1y2=-2，
∴
+
=-2，∴-5k2-12=-8k2-6，解得 k2=2，∴k=±
，
∴直线l方程为：
x-y-
=0，或
x+y-
=0．
设M（x1，y1），N（x2，y2），则x1，x2是方程的两个根，
由韦达定理得：x1+x2=
| 2a2 |
| a2+b2 |
| a2-a2•b2 |
| a2+b2 |
y1+y2=x1+x2-2=
| -2b2 |
| a2+b2 |
| x1+x2 |
| 2 |
| a2 |
| a2+b2 |
| y1+y2 |
| 2 |
| -b2 |
| a2+b2 |
∴kOP =
| yp |
| xp |
| b2 |
| a2 |
| 3 |
| 4 |
在直线l的方程中令y=0得，x=1，∴F（1，0），∴c=1．
解得：a2=4，b2=3，∴椭圆方程为：
| x2 |
| 4 |
| y2 |
| 3 |
（2）联立方程组：
|
∵△=（-8k2）2-4（4k2+3）（ 4k2-12）=144（k2+1）＞0，
x1+x2=
| 8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
∴y1+y2=k（x1+x2-2）=
| -6k |
| 4k2+3 |
| -9k2 |
| 4k2+3 |
再由 A1（-2，0），A2（2，0），M（x1，y1），N（x2，y2），
| A1N |
| MA2 |
| A1M |
| NA2 |
由
| A1N |
| MA2 |
| A1M |
| NA2 |
花间得-2x1x2-2y1y2+8=12，∴x1x2+y1y2=-2，
∴
| 4k2-12 |
| 4k2+3 |
| -92 |
| 4k2+3 |
| 2 |
∴直线l方程为：
| 2 |
| 2 |
| 2 |
| 2 |
点评：本题主要考查椭圆的标准方程、性质，直线和圆锥曲线的位置关系、韦达定理、两个向量的数量积公式，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
设sinθ=
（m＞0），则cos（θ+
）的取值范围是（ ）
| m2+1 |
| 4m |
| π |
| 6 |
A、[-1，
| ||||||
B、[-1，
| ||||||
C、[-
| ||||||
D、[-
|
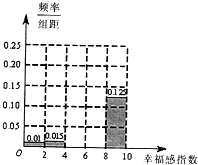“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时，给出的区间内的一个数，该数越接近10表示越满意，为了解某大城市市民的幸福感，随机对该城市的男、女各500人市民进行了调查，调查数据如下表所示：