题目内容
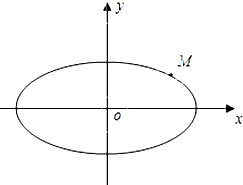 已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍,且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.
已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍,且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),l交椭圆于A、B两个不同点.(1)求椭圆的方程;
(2)求证直线MA、MB与x轴始终围成一个等腰三角形.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆方程为
+
=1(a>b>0),由题意可得:
,解得即可.
(2)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可.设A(x1,y1),B(x2,y2)直线l:y=
x+m,与椭圆方程联立可得x2+2mx+2m2-4=0,
利用斜率计算公式与跟与系数的关系可得:k1+k2=
+
=
,计算其分子=0即可.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可.设A(x1,y1),B(x2,y2)直线l:y=
| 1 |
| 2 |
利用斜率计算公式与跟与系数的关系可得:k1+k2=
| y1-1 |
| x1-1 |
| y2-1 |
| x2-1 |
| (y1-1)(x2-2)+(y2-1)(x1-2) |
| (x1-2)(x2-2) |
解答:
(1)解:设椭圆方程为
+
=1(a>b>0),
由题意可得:
,解得a2=8,b2=2.
∴椭圆方程为
+
=1.
(2)证明:设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可.
设A(x1,y1),B(x2,y2)直线l:y=
x+m,
则k1=
,k2=
.
联立方程
,得x2+2mx+2m2-4=0,
∴x1+x2=-2m,x1x2=2m2-4.
而k1+k2=
+
=
,
其分子=(
x1+m-1)(x2-2)+(
x2+m-1)(x1-2)
=x1x2+(m-2)(x1+x2)-4(m-1)=2m2-4-2m(m-2)-4m+4=0,
∴k1+k2=0.
故直线MA、MB与x轴始终围成一个等腰三角形.
| x2 |
| a2 |
| y2 |
| b2 |

由题意可得:
|
∴椭圆方程为
| x2 |
| 8 |
| y2 |
| 2 |
(2)证明:设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可.
设A(x1,y1),B(x2,y2)直线l:y=
| 1 |
| 2 |
则k1=
| y1-1 |
| x1-1 |
| y2-1 |
| x2-1 |
联立方程
|
∴x1+x2=-2m,x1x2=2m2-4.
而k1+k2=
| y1-1 |
| x1-1 |
| y2-1 |
| x2-1 |
| (y1-1)(x2-2)+(y2-1)(x1-2) |
| (x1-2)(x2-2) |
其分子=(
| 1 |
| 2 |
| 1 |
| 2 |
=x1x2+(m-2)(x1+x2)-4(m-1)=2m2-4-2m(m-2)-4m+4=0,
∴k1+k2=0.
故直线MA、MB与x轴始终围成一个等腰三角形.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得该协议书的关系、斜率计算公式、等腰三角形的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
函数f(x)=
+lg(3x+1)的定义域为( )
| 2x2 | ||
|
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-∞,
|
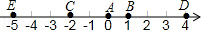 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样移动解答:
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样移动解答: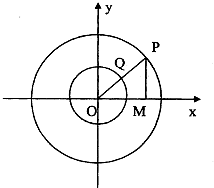 以原点为圆心的两个同心圆的方程分别为x2+y2=4和x2+y2=1,过原点O的射线交大圆于点P,交小圆于点Q,作PM⊥x轴于M,若
以原点为圆心的两个同心圆的方程分别为x2+y2=4和x2+y2=1,过原点O的射线交大圆于点P,交小圆于点Q,作PM⊥x轴于M,若 如图,焦点在x轴的椭圆C:
如图,焦点在x轴的椭圆C: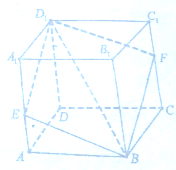 如图,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的平面分别交AA1,CC1于点E,F.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的平面分别交AA1,CC1于点E,F.