题目内容
 已知函数f(x)=
已知函数f(x)=
|
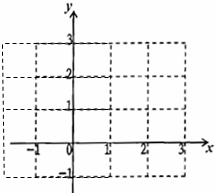
(1)在给出的平面直角坐标系中作出函数y=f(x)的图象;
(2)根据图象,写出该函数的单调区间;
(3)若集合A={x∈R|f(x)=a}中恰有三个元素,求实数a的取值范围.
考点:分段函数的应用
专题:函数的性质及应用
分析:(1)根据分段函数的解析式,分段画出函数图象即可;
(2)根据函数图象,从左向右呈“上升”趋势的为单调递增,呈“下降”趋势的即为单调递减,从而可得答案;
(3)根据题意,即求f(x)=a有三个不同的根,利用数形结合法,即可求得实数a的取值范围.
(2)根据函数图象,从左向右呈“上升”趋势的为单调递增,呈“下降”趋势的即为单调递减,从而可得答案;
(3)根据题意,即求f(x)=a有三个不同的根,利用数形结合法,即可求得实数a的取值范围.
解答:
解:(1)∵ 函数f(x)=
函数f(x)=
,
故在直角坐标系中作出图象如右图所示;
(2)由(1)所作出的图象可知,
从左向右呈“上升”趋势的为单调递增,呈“下降”趋势的即为单调递减,
故f(x)的单调区间为(-∞,0),(0,1),(1,+∞);
(3)集合A={x∈R|f(x)=a}中恰有三个元素,即为f(x)=a恰有三个不同的根,
故函数y=f(x)的图象与y=a的图象有三个不同的交点,
根据图象可知,实数a的取值范围为-1<a<0,
故实数a的取值范围为a∈(-1,0).

 函数f(x)=
函数f(x)=
|
故在直角坐标系中作出图象如右图所示;
(2)由(1)所作出的图象可知,
从左向右呈“上升”趋势的为单调递增,呈“下降”趋势的即为单调递减,
故f(x)的单调区间为(-∞,0),(0,1),(1,+∞);
(3)集合A={x∈R|f(x)=a}中恰有三个元素,即为f(x)=a恰有三个不同的根,
故函数y=f(x)的图象与y=a的图象有三个不同的交点,
根据图象可知,实数a的取值范围为-1<a<0,
故实数a的取值范围为a∈(-1,0).

点评:本题考查了分段函数的图象,分段函数的单调性以及分段函数的应用.对于分段函数的问题,一般选用分类讨论和数形结合的思想方法进行求解,根据分段函数的图象很容易得到相关的性质,若选用分类讨论的方法,则关键是讨论需用哪段解析式进行求解.同时也考查了函数的零点问题,函数的零点等价于对应方程的根,等价于函数的图象与x轴交点的横坐标,解题时要注意根据题意合理的选择转化.运用了数形结合的数学思想方法.属于中档题.

练习册系列答案
相关题目
一个三棱锥的各棱长均相等,其内部有一个内切球,即球与三棱锥的各面均相切(球在三棱锥的内部,且球与三棱锥的各面只有一个交点),过一条侧棱和对边的中点作三棱锥的截面,所得截面图形是( )
A、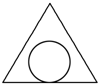 |
B、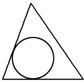 |
C、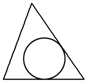 |
D、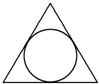 |
四边形ABCD为正方形,E为CD边的中点,且
=
,
=
,则
等于( )
| AB |
| a |
| AD |
| b |
| BE |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
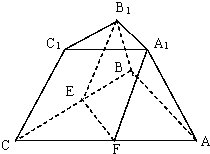 在上、下底面对应边之比为1:2的正三棱台中,过上底面一边A1B1作一个平行于棱的平面A1B1 EF,求这个平面分三棱台所成的两部分体积之比.
在上、下底面对应边之比为1:2的正三棱台中,过上底面一边A1B1作一个平行于棱的平面A1B1 EF,求这个平面分三棱台所成的两部分体积之比.