题目内容
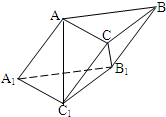 如图,三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,∠AA1B1为锐角,且侧面ABB1A1⊥底面ABC,给出下列四个结论:
如图,三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,∠AA1B1为锐角,且侧面ABB1A1⊥底面ABC,给出下列四个结论:①∠ABB1=60°;②AC⊥BB1;③直线AC1与平面ABB1A1所成的角为45°;④B1C⊥AC1.其中正确的结论是( )
| A、①③ | B、②④ |
| C、①③④ | D、①②③④ |
考点:直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:由题意知∠ABB1=∠AA1B1=60°;AC与BB1所在成角是60°;过A作AO⊥A1B1,连结C1O,∠C1AO是直线AC1与平面ABB1A1所成的角,C1O=AO=
,所以直线AC1与平面ABB1A1所成的角为45°;以O为原点,OC1为x轴,OB1为y轴,OA1为z轴,建立空间直角坐标系,利用向量法能求出B1C⊥AC1.
| 3 |
解答:
解:由题意知四边形AA1B1B是平行四边形,且∠AA1B1=60°,
∴∠ABB1=∠AA1B1=60°,故①正确;
∵AC∥A1C1,BB1∥AA1,∠AA1C1=60°,
∴AC与BB1所在成角是60°,故②错误;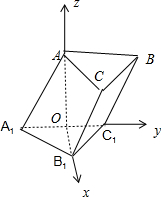
过A作AO⊥A1B1,连结C1O,
∵侧面ABB1A1⊥底面ABC,∴AO⊥面A1B1C1,
∴∠C1AO是直线AC1与平面ABB1A1所成的角,
∵∠ABB1=∠C1A1O=60°,A1C1=AA1=2,
∴C1O=AO=2sin60°=
,
∴∠C1A1O=45°,即直线AC1与平面ABB1A1所成的角为45°,故③正确;
以O为原点,OC1为x轴,OB1为y轴,OA1为z轴,建立空间直角坐标系,
则A(0,0,
),C1(
,0,0),B1(0,1,0),C(
,1,
),
∴
=(
,0,
),
=(
,0,-
),
∴
•
=0,∴B1C⊥AC1,故④正确.
故选:C.
∴∠ABB1=∠AA1B1=60°,故①正确;
∵AC∥A1C1,BB1∥AA1,∠AA1C1=60°,
∴AC与BB1所在成角是60°,故②错误;

过A作AO⊥A1B1,连结C1O,
∵侧面ABB1A1⊥底面ABC,∴AO⊥面A1B1C1,
∴∠C1AO是直线AC1与平面ABB1A1所成的角,
∵∠ABB1=∠C1A1O=60°,A1C1=AA1=2,
∴C1O=AO=2sin60°=
| 3 |
∴∠C1A1O=45°,即直线AC1与平面ABB1A1所成的角为45°,故③正确;
以O为原点,OC1为x轴,OB1为y轴,OA1为z轴,建立空间直角坐标系,
则A(0,0,
| 3 |
| 3 |
| 3 |
| 3 |
∴
| B1C |
| 3 |
| 3 |
| AC1 |
| 3 |
| 3 |
∴
| B1C |
| AC1 |
故选:C.
点评:本题以三棱柱为载体,考查空间角、空间直线的位置关系的判断,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
在极坐标系中,点(2,
)到直线ρ(
cosθ+sinθ)=2的距离为( )
| π |
| 6 |
| 3 |
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=
,则φ的值为( )
| π |
| 8 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
若a>b,则下列各项正确的是( )
| A、ac>bc |
| B、ax2>bx2 |
| C、a2>b2 |
| D、a2x>b2x |
已知i是虚数单位,则
=( )
| i2(-1+i) |
| 1+i |
| A、-1 | B、1 | C、-i | D、i |
在空间直角坐标系中,点P(3,-2,1)关于y对称的点的坐标是( )
| A、(3,2,-1) |
| B、(-3,-2,-1) |
| C、(-3,2,-1) |
| D、(-3,2,-1) |
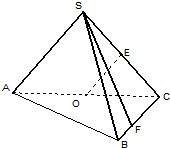 如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=
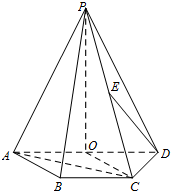 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,CD⊥平面PAD,BC∥AD,PA=PD,O,E分别为AD,PC的中点,PO=AD=2BC=2CD.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,CD⊥平面PAD,BC∥AD,PA=PD,O,E分别为AD,PC的中点,PO=AD=2BC=2CD.