题目内容
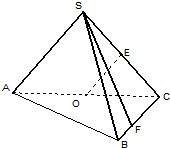 如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=| 2 |
| 1 |
| 2 |
(1)若点F在线段BC上,问:无论F在BC的何处,是否都有OE⊥SF?请证明你的结论;
(2)求二面角B-AS-C的平面角的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的性质
专题:综合题,空间位置关系与距离,空间角
分析:(1)由平面SAC⊥平面ABC,结合面面垂直的性质定理可得BC⊥平面ASC,可得BC⊥OE结合OE⊥SC及线面垂直的判定定理可得:OE⊥平面BSC,再由线面垂直的性质可得无论F在BC的何处,都有OE⊥SF
(2)由(1)中BC⊥平面ASC,可得AS⊥平面BCS,进而AS⊥SB,即∠BSC是二面角B-AS-C的平面角,解Rt△BCS可得二面角B-AS-C的平面角的余弦值.
(2)由(1)中BC⊥平面ASC,可得AS⊥平面BCS,进而AS⊥SB,即∠BSC是二面角B-AS-C的平面角,解Rt△BCS可得二面角B-AS-C的平面角的余弦值.
解答:
解:(1)在△SAB中,
∵OE∥AS,∠ASC=90°
∴OE⊥SC
∵平面SAC⊥平面ABC,∠BCA=90°
∴BC⊥平面ASC,OE?平面ASC
∴BC⊥OE
∴OE⊥平面BSC
∵SF?平面BSC
∴OE⊥SF
∴无论F在BC的何处,都有OE⊥SF
(2)由(1)BC⊥平面ASC
∴BC⊥AS
又∵∠ASC=90°
∴AS⊥SC
∴AS⊥平面BCS
∴AS⊥SB
∴∠BSC是二面角B-AS-C的平面角
在Rt△BCS中,cos∠BSC=
∴二面角B-AS-C的平面角的余弦值为
.
∵OE∥AS,∠ASC=90°
∴OE⊥SC
∵平面SAC⊥平面ABC,∠BCA=90°
∴BC⊥平面ASC,OE?平面ASC
∴BC⊥OE
∴OE⊥平面BSC
∵SF?平面BSC
∴OE⊥SF
∴无论F在BC的何处,都有OE⊥SF
(2)由(1)BC⊥平面ASC
∴BC⊥AS
又∵∠ASC=90°
∴AS⊥SC
∴AS⊥平面BCS
∴AS⊥SB
∴∠BSC是二面角B-AS-C的平面角
在Rt△BCS中,cos∠BSC=
| ||
| 3 |
∴二面角B-AS-C的平面角的余弦值为
| ||
| 3 |
点评:本题考查的知识点是二面角的平面角及其求法,直线与平面垂直的性质,其中(1)的关键是熟练掌握空间线面垂直的判定定理,性质定理及几何特征;(2)的关键是构造出二面角的平面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列两个量之间的关系是相关关系的是( )
| A、学生的成绩和体重 |
| B、匀速直线运动的物体时间与位移的关系 |
| C、水的体积和重量 |
| D、路上疲劳驾驶的人数和交通事故发生的多少 |
曲线y=
在点(0,0)处的切线方程为( )
| x |
| x+2 |
| A、y=2x | ||
| B、y=2x-2 | ||
C、y=
| ||
D、y=
|

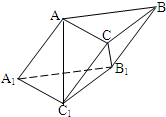 如图,三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,∠AA1B1为锐角,且侧面ABB1A1⊥底面ABC,给出下列四个结论:
如图,三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,∠AA1B1为锐角,且侧面ABB1A1⊥底面ABC,给出下列四个结论: