题目内容
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=
,则φ的值为( )
| π |
| 8 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
考点:正弦函数的对称性
专题:三角函数的求值
分析:利用正弦函数的对称性易求φ=kπ+
(k∈Z),又-π<φ<0,从而可得答案.
| π |
| 4 |
解答:
解:∵直线x=
是函数f(x)=sin(2x+φ)的一条对称轴,
∴2×
+φ=kπ+
(k∈Z),
∴φ=kπ+
(k∈Z),又-π<φ<0,
∴当k=-1时,φ=-
,
故选:C.
| π |
| 8 |
∴2×
| π |
| 8 |
| π |
| 2 |
∴φ=kπ+
| π |
| 4 |
∴当k=-1时,φ=-
| 3π |
| 4 |
故选:C.
点评:本题考查正弦函数的对称性,求得φ=kπ+
(k∈Z)是关键,属于中档题.
| π |
| 4 |

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
曲线y=
在点(0,0)处的切线方程为( )
| x |
| x+2 |
| A、y=2x | ||
| B、y=2x-2 | ||
C、y=
| ||
D、y=
|
已知在△ABC中,BC=6,AB=4,cosB=
,则AC=( )
| 1 |
| 3 |
| A、6 | ||
B、2
| ||
C、3
| ||
D、4
|
cos(α-β)cosβ-sin(α-β)sinβ化简的结果是( )
| A、sin(2α+β) |
| B、cos(α-2β) |
| C、cosα |
| D、cosβ |
已知函数f(x),当自变量x由x0增加到x0+△x时,函数值的增量与自变量的增量的比值为( )
| A、函数在x0处的变化率 |
| B、函数在区间[x0,x0+△x]上的平均变化率 |
| C、函数在x0+△x处的变化率 |
| D、函数在x0处的导数 |
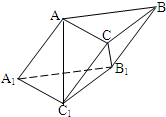 如图,三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,∠AA1B1为锐角,且侧面ABB1A1⊥底面ABC,给出下列四个结论:
如图,三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,∠AA1B1为锐角,且侧面ABB1A1⊥底面ABC,给出下列四个结论:①∠ABB1=60°;②AC⊥BB1;③直线AC1与平面ABB1A1所成的角为45°;④B1C⊥AC1.其中正确的结论是( )
| A、①③ | B、②④ |
| C、①③④ | D、①②③④ |
下列函数中,最小值为6的是( )
A、y=x+
| ||
| B、y=ex+9•e-x | ||
C、y=sinx+
| ||
| D、y=log2x+9logx2 |
若a>0,b>0且4a2+b2=4,则a
的最大值是( )
| 1+b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|