题目内容
若a＞b，则下列各项正确的是（ ）
| A、ac＞bc |
| B、ax2＞bx2 |
| C、a2＞b2 |
| D、a2x＞b2x |
考点：不等式的基本性质
专题：不等式的解法及应用
分析：A．c≤0时，不成立；
B．x=0时，不成立；
C.0≥a＞b时，不成立；
D．由2x＞0，a＞b，利用不等式的性质可得a•2x＞b•2x．
B．x=0时，不成立；
C.0≥a＞b时，不成立；
D．由2x＞0，a＞b，利用不等式的性质可得a•2x＞b•2x．
解答：
解：A．c≤0时，不成立；
B．x=0时，不成立；
C.0≥a＞b时，不成立；
D．∵2x＞0，a＞b，∴a•2x＞b•2x，成立．
故选：D．
B．x=0时，不成立；
C.0≥a＞b时，不成立；
D．∵2x＞0，a＞b，∴a•2x＞b•2x，成立．
故选：D．
点评：本题考查了不等式的基本性质，属于基础题．
练习册系列答案
习题精选系列答案
相关题目
下列说法中，正确的是（ ）
| A、命题“若am2＜bm2，则a＜b”的否命题是“若am2＞bm2，则a＞b” |
| B、命题“?x∈R，x2+x＞0”的否定是“?x∉R，x2+x≤0” |
| C、命题“a，b，c，d∈R，若a-c＞b-d且c＞d，则a＞b”是真命题 |
| D、已知x∈R，则“x＞0”是“x＞1”的充分不必要条件 |
cos（α-β）cosβ-sin（α-β）sinβ化简的结果是（ ）
| A、sin（2α+β） |
| B、cos（α-2β） |
| C、cosα |
| D、cosβ |
已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上是增函数．令a=f（sin
），b=f（cos
），c=f（tan
），则（ ）
| 5π |
| 7 |
| 2π |
| 7 |
| 2π |
| 7 |
| A、b＜a＜c |
| B、c＜b＜a |
| C、b＜c＜a |
| D、a＜b＜c |
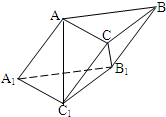如图，三棱柱ABC-A1B1C1的各棱长均为2，侧棱BB1与底面ABC所成的角为60°，∠AA1B1为锐角，且侧面ABB1A1⊥底面ABC，给出下列四个结论：①∠ABB1=60°；②AC⊥BB1；③直线AC1与平面ABB1A1所成的角为45°；④B1C⊥AC1．其中正确的结论是（ ）
| A、①③ | B、②④ |
| C、①③④ | D、①②③④ |
已知α∈（-
，0），cos（π+α）=-
，则tanα=（ ）
| π |
| 2 |
| 2 |
| 3 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
一个电路如图所示，A，B，C，D，E，F为6个开关，其闭合的概率都是| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|