题目内容
在空间直角坐标系中，点P（3，-2，1）关于y对称的点的坐标是（ ）
| A、（3，2，-1） |
| B、（-3，-2，-1） |
| C、（-3，2，-1） |
| D、（-3，2，-1） |
考点：空间中的点的坐标
专题：空间位置关系与距离
分析：在空间直角坐标系中，点（3，-2，1）关于y轴对称就是把x变为-x，z变为-z，y不变，从而求解；
解答：
解：∵在空间直角坐标系中，点（3，-2，1）关于y轴对称，
∴其对称点为：（-3，-2，-1），
故选：B．
∴其对称点为：（-3，-2，-1），
故选：B．
点评：此题主要考查空间直角坐标系，点的对称问题，点（x，y，z）关于y轴对称为（-x，y，-z），此题是一道基础题．
练习册系列答案
阅读快车系列答案
相关题目
曲线y=
在点（0，0）处的切线方程为（ ）
| x |
| x+2 |
| A、y=2x | ||
| B、y=2x-2 | ||
C、y=
| ||
D、y=
|
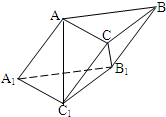如图，三棱柱ABC-A1B1C1的各棱长均为2，侧棱BB1与底面ABC所成的角为60°，∠AA1B1为锐角，且侧面ABB1A1⊥底面ABC，给出下列四个结论：①∠ABB1=60°；②AC⊥BB1；③直线AC1与平面ABB1A1所成的角为45°；④B1C⊥AC1．其中正确的结论是（ ）
| A、①③ | B、②④ |
| C、①③④ | D、①②③④ |
下列函数中，最小值为6的是（ ）
A、y=x+
| ||
| B、y=ex+9•e-x | ||
C、y=sinx+
| ||
| D、y=log2x+9logx2 |
一个电路如图所示，A，B，C，D，E，F为6个开关，其闭合的概率都是| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
平行于同一条直线的两条直线间的位置关系是（ ）
| A、异面 | B、平行 |
| C、相交 | D、以上都有可能 |
已知回归直线方程的斜率的估计值是1.2，样本的中心点为（2，3），则回归直线方程是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若a＞0，b＞0且4a2+b2=4，则a
的最大值是（ ）
| 1+b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
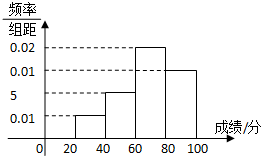学校组织学生参加模块测试，测试后随机抽查部分学生的成绩，成绩的频率分布直方图如图5，数据的分组依次为[20，40），[40，60），[60，80），[80，100]，低于60分的人数是6人