题目内容
在极坐标系中，点(2，
)到直线ρ(
cosθ+sinθ)=2的距离为（ ）
| π |
| 6 |
| 3 |
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
考点：简单曲线的极坐标方程
专题：选作题,坐标系和参数方程
分析：根据所给的直线的极坐标方程，转化成直线的一般式方程，根据点到直线的距离，写出距离的表示式，得到结果．
解答：
解：直线ρ(
cosθ+sinθ)=2的一般式方程是：
x+y-2=0，点(2，
)的直角坐标为（
，1）
∴点（
，1）到直线的距离是
=1
故选：D．
| 3 |
| 3 |
| π |
| 6 |
| 3 |
∴点（
| 3 |
| |3+1-2| |
| 2 |
故选：D．
点评：本题考查点到直线的距离公式和简单的极坐标方程，本题解题的关键是把极坐标方程转化成一般式方程．
练习册系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
下列两个量之间的关系是相关关系的是（ ）
| A、学生的成绩和体重 |
| B、匀速直线运动的物体时间与位移的关系 |
| C、水的体积和重量 |
| D、路上疲劳驾驶的人数和交通事故发生的多少 |
曲线y=
在点（0，0）处的切线方程为（ ）
| x |
| x+2 |
| A、y=2x | ||
| B、y=2x-2 | ||
C、y=
| ||
D、y=
|
下列说法中，正确的是（ ）
| A、命题“若am2＜bm2，则a＜b”的否命题是“若am2＞bm2，则a＞b” |
| B、命题“?x∈R，x2+x＞0”的否定是“?x∉R，x2+x≤0” |
| C、命题“a，b，c，d∈R，若a-c＞b-d且c＞d，则a＞b”是真命题 |
| D、已知x∈R，则“x＞0”是“x＞1”的充分不必要条件 |
已知在△ABC中，BC=6，AB=4，cosB=
，则AC=（ ）
| 1 |
| 3 |
| A、6 | ||
B、2
| ||
C、3
| ||
D、4
|
cos（α-β）cosβ-sin（α-β）sinβ化简的结果是（ ）
| A、sin（2α+β） |
| B、cos（α-2β） |
| C、cosα |
| D、cosβ |
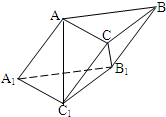如图，三棱柱ABC-A1B1C1的各棱长均为2，侧棱BB1与底面ABC所成的角为60°，∠AA1B1为锐角，且侧面ABB1A1⊥底面ABC，给出下列四个结论：①∠ABB1=60°；②AC⊥BB1；③直线AC1与平面ABB1A1所成的角为45°；④B1C⊥AC1．其中正确的结论是（ ）
| A、①③ | B、②④ |
| C、①③④ | D、①②③④ |
已知回归直线方程的斜率的估计值是1.2，样本的中心点为（2，3），则回归直线方程是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
