题目内容
某人步行晨练,先快步走了一段,后慢速行走了一段.下面四个图象中(纵轴d均表示行走的路程,横轴t均表示行走的时间),符合他走法的是( )
A、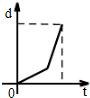 |
B、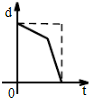 |
C、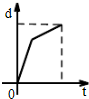 |
D、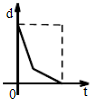 |
考点:函数的图象
专题:函数的性质及应用
分析:由路程与时间的关系来分析,当速度快时,路程随时间的增加而增加的快,图象表现为“陡峭”,相反,当速度慢时,路程随时间增加而增加的慢,图象表现为“平缓”,据此对四个图象进行判断.
解答:
解:由题意,随着时间的增加,路程随着增加,所以d一定是关于t的增函数,故排除B、D两项;
而该人先快步走了一段,后慢速行走了一段,所以一开始速度快,即单位时间内路程的增加量大,图象表现为“陡峭”,后面走得慢,速度小,图象“平缓”,显然C项满足题意.
故选:C.
而该人先快步走了一段,后慢速行走了一段,所以一开始速度快,即单位时间内路程的增加量大,图象表现为“陡峭”,后面走得慢,速度小,图象“平缓”,显然C项满足题意.
故选:C.
点评:本题主要是考查了如何用函数图象体现函数值相对于自变量的变化率的问题.一般来说,当变化率大时,图象表现为“陡峭”,反之,则图象“平缓”.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列两个量之间的关系是相关关系的是( )
| A、学生的成绩和体重 |
| B、匀速直线运动的物体时间与位移的关系 |
| C、水的体积和重量 |
| D、路上疲劳驾驶的人数和交通事故发生的多少 |
cos(α-β)cosβ-sin(α-β)sinβ化简的结果是( )
| A、sin(2α+β) |
| B、cos(α-2β) |
| C、cosα |
| D、cosβ |
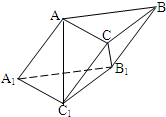 如图,三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,∠AA1B1为锐角,且侧面ABB1A1⊥底面ABC,给出下列四个结论:
如图,三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,∠AA1B1为锐角,且侧面ABB1A1⊥底面ABC,给出下列四个结论:①∠ABB1=60°;②AC⊥BB1;③直线AC1与平面ABB1A1所成的角为45°;④B1C⊥AC1.其中正确的结论是( )
| A、①③ | B、②④ |
| C、①③④ | D、①②③④ |
已知α∈(-
,0),cos(π+α)=-
,则tanα=( )
| π |
| 2 |
| 2 |
| 3 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
下列函数中,最小值为6的是( )
A、y=x+
| ||
| B、y=ex+9•e-x | ||
C、y=sinx+
| ||
| D、y=log2x+9logx2 |
 一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是
一个电路如图所示,A,B,C,D,E,F为6个开关,其闭合的概率都是| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知回归直线方程的斜率的估计值是1.2,样本的中心点为(2,3),则回归直线方程是( )
A、
| ||
B、
| ||
C、
| ||
D、
|

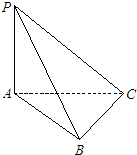 如图,已知PA⊥平面ABC,AB⊥BC,若PA=2,AB=1,BC=
如图,已知PA⊥平面ABC,AB⊥BC,若PA=2,AB=1,BC=