题目内容
对实数a和b，定义运算“?”：a?b=
，设函数f（x）=x2?（x+2），x∈R，若函数y=f（x）-c的图象与x轴恰有三个公共点，则实数c的取值范围是（ ）
|
| A、[-1，0） |
| B、（0，1） |
| C、（-1，0） |
| D、（-1，0）∪[1，+∞） |
考点：函数的图象
专题：函数的性质及应用
分析：先根据依题意确定函数f（x）的解析式，画出函数图象，通过观察确定c的范围．
解答：
解：当x2≤x+2时，即-1≤x≤2时，f（x）=x2，
当x2＞x+2时，即x＞2或x＜-1，f（x）=x+2，
函数图象如图：
，
y=f（x）-c的图象是由函数f（x）向下平移c个单位获得的，如图，函数图象与x轴恰有三个交点，
当函数f（x）向下平移一个单位后，函数图象与x轴恰有三个交点，
故0≤c≤1
故选B．
当x2＞x+2时，即x＞2或x＜-1，f（x）=x+2，
函数图象如图：
，y=f（x）-c的图象是由函数f（x）向下平移c个单位获得的，如图，函数图象与x轴恰有三个交点，
当函数f（x）向下平移一个单位后，函数图象与x轴恰有三个交点，
故0≤c≤1
故选B．
点评：本题主要考查了函数图象与性质，函数图象的平移，分段函数的应用．注重了对数形结合的思想的运用．
练习册系列答案
相关题目
已知函数y=x3+ax在区间（-∞，1）上为减函数，在（1，+∞）上为增函数，则a的值为（ ）
| A、3 | ||
| B、-3 | ||
C、-
| ||
D、
|
若点P为双曲线
-
=1（a＞0，b＞0）上任意一点，过点P作双曲线两渐近线的平行线，分别与两渐近线交于M，N两点，若|PM|•|PN|=b2，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
下列命题正确的是（ ）
| A、a∥b，a⊥α⇒a⊥b |
| B、a⊥α，b⊥α⇒a∥b |
| C、a⊥α，a⊥b⇒b∥α |
| D、a∥α，a⊥b⇒b⊥α |
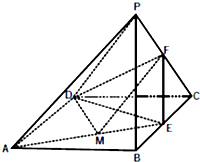如图，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，且∠DAB=60°，PA=PD=