题目内容
在四边形ABCD中，已知AB=9，BC=6，
=2
．
（1）若四边形ABCD是矩形，求
•
的值；
（2）若四边形ABCD是平行四边形，且
•
=6，求
与
夹角的余弦值．
| CP |
| PD |
（1）若四边形ABCD是矩形，求
| AP |
| BP |
（2）若四边形ABCD是平行四边形，且
| AP |
| BP |
| AB |
| AD |
考点：数量积表示两个向量的夹角,平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）由条件求出|
|=6，|
|=3，再用向量AB，AD表示向量AP，BP，再将数量积
•
展开，运用向量的平方为模的平方以及
•
=0，即可求出结果；
（2）设
与
夹角为θ，根据得到的数量积
•
，运用数量积定义，代入数据，即可求出cosθ．
| CP |
| DP |
| AP |
| BP |
| AB |
| AD |
（2）设
| AB |
| AD |
| AP |
| BP |
解答：
解：（1）∵四边形ABCD是矩形，
∴
⊥
，即
•
=0，
又AB=9，BC=6，
=2
，
∴|
|=6，|
|=3，
∵
=
+
=
+
，
=
-
=
-
，
∴
•
=（
+
）•（
-
）
=
2-
•
-
2
=62-
×92=18；
（2）设
与
夹角为θ，由（1）得，
•
=（
+
）•（
-
）
=
2-
•
-
2
=62-
×9×6•cosθ-
×92=6，
∴cosθ=
．
∴
| AB |
| AD |
| AB |
| AD |
又AB=9，BC=6，
| CP |
| PD |
∴|
| CP |
| DP |
∵
| AP |
| AD |
| DP |
| AD |
| 1 |
| 3 |
| AB |
| BP |
| BC |
| PC |
| AD |
| 2 |
| 3 |
| AB |
∴
| AP |
| BP |
| AD |
| 1 |
| 3 |
| AB |
| AD |
| 2 |
| 3 |
| AB |
=
| AD |
| 1 |
| 3 |
| AB |
| AD |
| 2 |
| 9 |
| AB |
=62-
| 2 |
| 9 |
（2）设
| AB |
| AD |
| AP |
| BP |
| AD |
| 1 |
| 3 |
| AB |
| AD |
| 2 |
| 3 |
| AB |
=
| AD |
| 1 |
| 3 |
| AB |
| AD |
| 2 |
| 9 |
| AB |
=62-
| 1 |
| 3 |
| 2 |
| 9 |
∴cosθ=
| 2 |
| 3 |
点评：本题主要考查两向量的数量积的定义，考查向量的平方等于模的平方，以及向量共线、垂直的条件，考查向量的运算求解能力．
练习册系列答案
相关题目
设A（-2，
），椭圆3x2+4y2=48的右焦点是F，点P在椭圆上移动，当|AP|+2|PF|取最小值时P点的坐标是（ ）
| 3 |
A、（0，2
| ||||
B、（0，-2
| ||||
C、（2
| ||||
D、（-2
|
下列命题正确的是（ ）
| A、a∥b，a⊥α⇒a⊥b |
| B、a⊥α，b⊥α⇒a∥b |
| C、a⊥α，a⊥b⇒b∥α |
| D、a∥α，a⊥b⇒b⊥α |
函数f（x）=lgx+x-3的零点所在的区间是（ ）
| A、（1，2） |
| B、（3，4） |
| C、（2，3） |
| D、（0，1） |
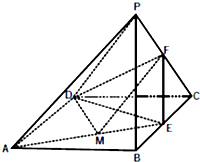如图，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，且∠DAB=60°，PA=PD=
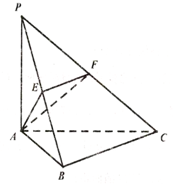如图，在三棱锥P-ABC中，∠ABC=90°，PA⊥平面ABC，E，F分别为PB，PC的中点．