题目内容
定义在R上的函数f(x)满足f(x)=
,则f(2014)的值是( )
|
| A、-1 |
| B、1 |
| C、log23 |
| D、-log23 |
考点:对数的运算性质
专题:函数的性质及应用
分析:f(2014)=f(2013)-f(2012)=[f(2012)-f(2011)]-f(2012)=-f(2011),即当x>6时满足f(x)=-f(x-3)=f(x-6),周期为6,由此能求出结果.
解答:
解:∵f(x)=
,
∵f(2014)=f(2013)-f(2012)
=[f(2012)-f(2011)]-f(2012)=-f(2011),
即当x>6时满足f(x)=-f(x-3)=f(x-6),周期为6
∴f(2014)=f(335×6+4)=f(4)
=f(3)-f(2)=f(2)-f(1)-f(2)=-f(1)
=-f(0)+f(-1)
=-log21+log22=1.
故选:B.
|
∵f(2014)=f(2013)-f(2012)
=[f(2012)-f(2011)]-f(2012)=-f(2011),
即当x>6时满足f(x)=-f(x-3)=f(x-6),周期为6
∴f(2014)=f(335×6+4)=f(4)
=f(3)-f(2)=f(2)-f(1)-f(2)=-f(1)
=-f(0)+f(-1)
=-log21+log22=1.
故选:B.
点评:本题考查分段函数的函数值的求法,是基础题,解题时要认真审题,注意函数的周期性的灵活运用.

练习册系列答案
相关题目
观察下列算式:
13=1,
23=3+5,
33=7+9+11,
43=13+15+17+19,
…
若某数n3按上述规律展开后,发现等式右边含有“2013”这个数,则n=( )
13=1,
23=3+5,
33=7+9+11,
43=13+15+17+19,
…
若某数n3按上述规律展开后,发现等式右边含有“2013”这个数,则n=( )
| A、41 | B、43 | C、45 | D、47 |
直线2x-y+1=0不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数y=x3+ax在区间(-∞,1)上为减函数,在(1,+∞)上为增函数,则a的值为( )
| A、3 | ||
| B、-3 | ||
C、-
| ||
D、
|
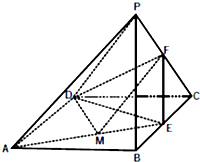 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=