题目内容
如图，已知ABCD是空间四边形，AB=AD，CB=CD，求证：BD⊥AC．考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：取BD的中点O，连接AO，CO．由等腰三角形的三线合一，得到AO⊥BD，CO⊥BD，再由线面垂直的判定定理得到BD⊥平面ACO，运用线面垂直的性质即可得证．
解答：
证明：
取BD的中点O，连接AO，CO．
∵AB=AD，∴AO⊥BD，
∵CB=CD，∴CO⊥BD，
又AO∩CO=O，
∴BD⊥平面ACO，
AC?平面ACO，
∴BD⊥AC．
取BD的中点O，连接AO，CO．∵AB=AD，∴AO⊥BD，
∵CB=CD，∴CO⊥BD，
又AO∩CO=O，
∴BD⊥平面ACO，
AC?平面ACO，
∴BD⊥AC．
点评：本题考查空间直线与平面的位置关系：垂直，考查线面垂直的判定和性质，属于基础题．
练习册系列答案
相关题目
直线2x-y+1=0不经过（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列命题正确的是（ ）
| A、a∥b，a⊥α⇒a⊥b |
| B、a⊥α，b⊥α⇒a∥b |
| C、a⊥α，a⊥b⇒b∥α |
| D、a∥α，a⊥b⇒b⊥α |
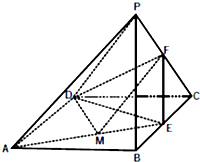如图，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，且∠DAB=60°，PA=PD=