题目内容
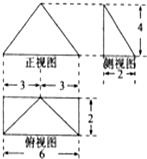
如图所示是四棱锥的三视图，则该几何的体积等于（ ）
| A、16 | ||
B、34+6
| ||
| C、6 | ||
D、17+6
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：一个底面是矩形的四棱锥，矩形的长和宽分别是6，2，底面上的高与底面交于底面一条边的中点，四棱锥的高是4，即可求解．
解答：
解：由三视图知，这是一个底面是矩形的四棱锥，
矩形的长和宽分别是6，2
底面上的高与底面交于底面一条边的中点，
四棱锥的高是4，
∴四棱锥的体积为：
×2×6×4=16．
故选A．
矩形的长和宽分别是6，2
底面上的高与底面交于底面一条边的中点，
四棱锥的高是4，
∴四棱锥的体积为：
| 1 |
| 3 |
故选A．
点评：本题考查由三视图求几何体的体积，考查由三视图还原几何体的直观图，考查平面图形体积的求法，本题是一个基础题．
练习册系列答案
相关题目
设奇函数f（x）的定义域为[-5，5]，若当x∈[0，5]时，f（x）的图象如图，则不等式f（x）≤0的解集为函数y=ln（2-x-x2）+
的定义域是（ ）
| 1 | ||
|
| A、（-1，2） |
| B、（-∞，-2）∪（1，+∞） |
| C、（-2，1） |
| D、[-2，1） |
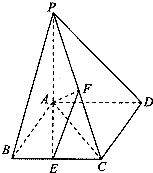如图，四棱锥P-ABCD的底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，直线PC与底面ABCD所成的角为45°，E、F分别是BC、PC的中点．