题目内容
解不等式:4≤|x2-4x|<5.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:去掉绝对值符号,原不等式转化为4≤x2-4x<5或-5<x2-4x≤-4,分别解之,最后取其并集即可.
解答:
解:∵4≤|x2-4x|<5,
∴4≤x2-4x<5①或4≤-(x2-4x)<5?-5<x2-4x≤-4②,
①式可转化为
,
解不等式x2-4x≥4得:2+2
≤x或x≤2-2
;
解不等式x2-4x<5得:-1<x<5;
∴4≤x2-4x<5的解为:2+2
≤x<5或-1<x≤2-2
;
②可转化为:
,
解不等式x2-4x>-5得:x∈R;
解不等式x2-4x≤-4得:x=2;
不等式组的解为:x=2.
综合①②知,
不等式4≤|x2-4x|<5的解集为:[2+2
,5)∪(-1,2-2
]∪{2}.
∴4≤x2-4x<5①或4≤-(x2-4x)<5?-5<x2-4x≤-4②,
①式可转化为
|
解不等式x2-4x≥4得:2+2
| 2 |
| 2 |
解不等式x2-4x<5得:-1<x<5;
∴4≤x2-4x<5的解为:2+2
| 2 |
| 2 |
②可转化为:
|
解不等式x2-4x>-5得:x∈R;
解不等式x2-4x≤-4得:x=2;
不等式组的解为:x=2.
综合①②知,
不等式4≤|x2-4x|<5的解集为:[2+2
| 2 |
| 2 |
点评:本题考查绝对值不等式的解法,原不等式去掉绝对值符号,转化为4≤x2-4x<5或-5<x2-4x≤-4是关键,考查转化思想与方程思想,考查运算能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
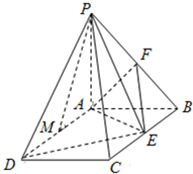 如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=
如图,已知PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,AD=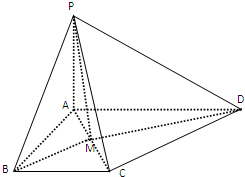 如图所示,PA⊥平面ABCD,△CAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.
如图所示,PA⊥平面ABCD,△CAB为等边三角形,PA=AB,AC⊥CD,M为AC中点.