题目内容
将函数f(x)=
sinx-cosx的图象向右平移φ(φ>0)个单位,所得图象对应的函数为奇函数,则φ的最小值为 .
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:利用和差角公式,可将函数f(x)的解析式化为正弦型函数的形式,结合函数图象的平称变换法则,可得平移后函数的解析式,结合平移后函数为奇函数,则其初相角终边必落在x轴上,可得φ的表达式,进而求出φ的最小值.
解答:
解:因为f(x)=
sinx-cosx=2sin(x-
),
f(x)的图象向右平移φ个单位所得图象对应的函数解析式
y=2sin(x-
-φ)φ>0,
若所得函数为奇函数,
sin(-
-φ)=0
∴φ=-
+kπ,k∈Z
当k=1时,φ取最小值为
.
故答案为:
| 3 |
| π |
| 6 |
f(x)的图象向右平移φ个单位所得图象对应的函数解析式
y=2sin(x-
| π |
| 6 |
若所得函数为奇函数,
sin(-
| π |
| 6 |
∴φ=-
| π |
| 6 |
当k=1时,φ取最小值为
| 5π |
| 6 |
故答案为:
| 5π |
| 6 |
点评:本题考查的知识点是函数图象的平移变换,正弦函数的奇偶性,熟练掌握正弦型函数的图象和性质是解答的关键.

练习册系列答案
相关题目
在数列{an}中,如果存在非零的常数T,使得an+T=an对于任意正整数n均成立,那么就称数列{an}为周期数列,其中T叫做数列{an}的周期.已知数列{xn}满足xn+2=|xn+1-xn|(x∈N*),若x1=1,x2=a(a≤1,a≠0),当数列{xn}的周期为3时,则数列{xn}的前2011项的和s2011为( )
| A、669 | B、670 |
| C、1338 | D、1341 |
若ax2+4ax+3≥0恒成立,a的取值范围是( )
A、(0,
| ||
B、(0,
| ||
C、[0,
| ||
D、[0,
|
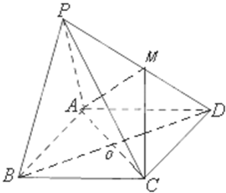 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知