Question

两条异面直线AB、CD分别在两平行平面α、β上，α、β间的距离为d，若三棱锥A-BCD为正四面体，则其体积为（　　）

• A、

  1

  3

  d³
• B、

  2

  3

  d³
• C、d³
• D、

  4

  3

  d³

Answer 1

考点：棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：分别取AB、CD中点E、F，连结AF，BF，由已知得EF是AB和CD的公垂线，从而EF=d，设正四面体A-BCD的棱长为a，作AO垂直于面BDC，求出AF，BF，OF，AO，由此能求出三棱锥A-BCD的体积．

解答： 解：分别取AB、CD中点E、F，连结AF，BF，
∵A-BCD是正四面体，∴AF=BF，∴EF⊥AB，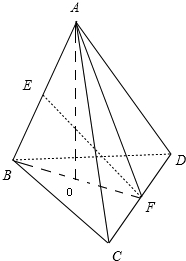
同理，EF⊥CD，∴EF是AB和CD的公垂线，
∵两条异面直线AB、CD分别在两平行平面α、β上，α、β间的距离为d，
∴EF=d，
设正四面体A-BCD的棱长为a，则AF=BF=

3

2

a，AE=BE=

a

2

，
∵AE²+EF²=AF²，∴

a2

4

+d2=

3

4

a2，∴a=

2

d，
作AO垂直于面BDC，交AF于O，
AF=BF=

3

2

a=

6

2

d，OF=

1

3

BF=

6

6

d，AO=

( 6 2 d)2-( 6 6 d)2

=

2 3

3

d，
∴三棱锥A-BCD的体积：
V=

1

3

S△BCD•AO=

1

3

×

1

2

×

2

d×

6

2

d×

2 3

3

d=

d3

3

．
故选：A．

点评：本题考查三棱锥的体积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．