题目内容
已知△ABC的角A，B，C所对的边分别为a，b，c，且acosB+
bsinA=c．
（Ⅰ）求角A的大小；
（Ⅱ）若a=1，
•
=3，求b+c的值．
| 3 |
（Ⅰ）求角A的大小；
（Ⅱ）若a=1，
| AB |
| AC |
考点：正弦定理,平面向量数量积的运算
专题：解三角形
分析：（Ⅰ）利用正弦定理把已知等式转化成角的正弦的关系式，整理求得tanA的值，进而求得A．
（Ⅱ）利用向量积的性质求得bc的值，进而利用余弦定理求得b2+c2的值，最后用配方法求得答案．
（Ⅱ）利用向量积的性质求得bc的值，进而利用余弦定理求得b2+c2的值，最后用配方法求得答案．
解答：
解：（Ⅰ）△ABC中，∵acosB+
bsinA=c，
∴sinAcosB+
sinBsinA=sinC，
∵sinC=sin（A+B）=sinAcosB+cosAsinB
∴sinAcosB+
sinBsinA=sinAcosB+cosAsinB
整理得
sinA=cosA，即tanA=
，
∴A=
．
（Ⅱ）AB•AC•cosA=|
•
|=3，
∴bc•
=3，即bc=2
，
∵a2=b2+c2-2bccosA，即1=b2+c2-2•2
•
，
∴b2+c2=1+6=7，
∴b+c=
=
．
| 3 |
∴sinAcosB+
| 3 |
∵sinC=sin（A+B）=sinAcosB+cosAsinB
∴sinAcosB+
| 3 |
整理得
| 3 |
| ||
| 3 |
∴A=
| π |
| 6 |
（Ⅱ）AB•AC•cosA=|
| AB |
| AC |
∴bc•
| ||
| 2 |
| 3 |
∵a2=b2+c2-2bccosA，即1=b2+c2-2•2
| 3 |
| ||
| 2 |
∴b2+c2=1+6=7，
∴b+c=
| b2+c2+2bc |
7+4
|
点评：本题主要考查了正弦定理和余弦定理的应用，向量积的运算．综合性很强．
练习册系列答案
相关题目
若P是抛物线x2=4y上的一个动点，则点P到直线l1：y=-1，l2：3x+4y+12=0的距离之和的最小值为（ ）
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
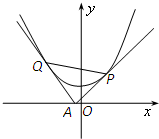过x轴上动点A（a，0），引抛物线y=x2+1的两条切线AP、AQ．切线斜率分别为k1和k2，切点分别为P、Q．