题目内容
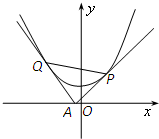 过x轴上动点A(a,0),引抛物线y=x2+1的两条切线AP、AQ.切线斜率分别为k1和k2,切点分别为P、Q.
过x轴上动点A(a,0),引抛物线y=x2+1的两条切线AP、AQ.切线斜率分别为k1和k2,切点分别为P、Q.(1)求证:k1•k2为定值;并且直线PQ过定点;
(2)记S为面积,当
| S△APQ | ||
|
|
| AP |
| AQ |
考点:利用导数研究曲线上某点切线方程,平面向量数量积的运算
专题:向量与圆锥曲线,圆锥曲线中的最值与范围问题
分析:(1)设出直线方程,与抛物线联立,由韦达定理得出:k1•k2的值;设出P、Q两点坐标,写出PQ方程,由根与系数关系代入并化简求出定点坐标;
(2)当
最小时,即A点到直线PQ的距离的最小值,利用基本不等式,求出a的值,代入
•
式子中即可.
(2)当
| S△APQ | ||
|
|
| AP |
| AQ |
解答:
解:(1)证明:易知切线的斜率存在,设过A点的直线为:y=k(x-a),
由
得:x2-kx+ka+1=0,△=k2-4ak-4=0,
∴k1+k2=4a,k1•k2=-4为定值.
由y=x2+1,得y'=2x,设切点P、Q坐标分别为P(xp,yp),Q(xQ,yQ),k1=2xp,k2=2xq
∴xp+xq=2a,xp•xq=-1,
PQ的直线方程:y-yp=
(x-xp),由yp=xp2+1,yq=xq2+1
得到y=(xp+xq)x-xp
+1
整理可得y=2xa+2,∴直线PQ过定点(0,2).
(2)解:设A到PQ的距离为d.则S△APQ=|PQ|×
,
∴
=
=
=
,
设t=
≥1,∴
=
≥
,
当且仅当t=
时取等号,即a=±
.
∵
•
=(xp-a,yp)•(xQ-a,yQ)=xpxQ-a(xp+xQ)+a2+ypyQ
又∵ypyQ=(2xpa+2)(2xQa+2)=4a2xpxQ+4+4a(xp+xQ)=4a2+4
所以
•
=3a2+3=
.
由
|
∴k1+k2=4a,k1•k2=-4为定值.
由y=x2+1,得y'=2x,设切点P、Q坐标分别为P(xp,yp),Q(xQ,yQ),k1=2xp,k2=2xq
∴xp+xq=2a,xp•xq=-1,
PQ的直线方程:y-yp=
| yp-yq |
| xp-xq |
得到y=(xp+xq)x-xp
| x | q |
整理可得y=2xa+2,∴直线PQ过定点(0,2).
(2)解:设A到PQ的距离为d.则S△APQ=|PQ|×
| d |
| 2 |
∴
| S△APQ |
| |PQ| |
| d |
| 2 |
| 2a2+2 | ||
2
|
| a2+1 | ||
|
设t=
| 4a2+1 |
| S△APQ |
| |PQ| |
| t2+3 |
| 4t |
| ||
| 2 |
当且仅当t=
| 3 |
| ||
| 2 |
∵
| AQ |
| AP |
又∵ypyQ=(2xpa+2)(2xQa+2)=4a2xpxQ+4+4a(xp+xQ)=4a2+4
所以
| AQ |
| AP |
| 9 |
| 2 |
点评:本题是考查直线与圆锥曲线相交、定点、定值、最值的问题,用到设而不求,韦达定理,基本不等式,等价转换等思想.是一道综合性非常强的圆锥曲线问题.

练习册系列答案
相关题目
已知某物体的运动曲线方程为:S=2t2-3t-1,则该物体在t=3时的速度为( )
| A、8 | B、9 | C、10 | D、11 |
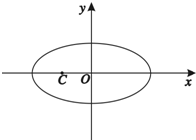 在平面直角坐标系xOy中,椭圆Γ:
在平面直角坐标系xOy中,椭圆Γ: