题目内容
已知直线l:
(t为参数);椭圆C1:
(θ为参数)
(Ⅰ)求直线l倾斜角的余弦值;
(Ⅱ)试判断直线l与椭圆C1的交点个数.
|
|
(Ⅰ)求直线l倾斜角的余弦值;
(Ⅱ)试判断直线l与椭圆C1的交点个数.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)参数方程化为普通方程,得斜率为-
,则倾斜角的余弦值可求;
(Ⅱ)极坐标方程化为直角坐标方程,联立方程组,即可得到结论.
| 3 |
| 4 |
(Ⅱ)极坐标方程化为直角坐标方程,联立方程组,即可得到结论.
解答:
解:(Ⅰ)将直线参数方程化为普通方程得:4x+3y=17,得斜率为-
,则倾斜角的余弦值为-
;
(Ⅱ)椭圆椭圆C1:的普通方程为:
+
=1
与4x+3y=17联立,消去y可得52x2-136x+145=0,
∴△<0,
∴没有交点.
| 3 |
| 4 |
| 3 |
| 5 |
(Ⅱ)椭圆椭圆C1:的普通方程为:
| x2 |
| 4 |
| y2 |
| 16 |
与4x+3y=17联立,消去y可得52x2-136x+145=0,
∴△<0,
∴没有交点.
点评:本题考查参数方程化为普通方程,极坐标方程化为直角坐标方程,考查直线与椭圆的位置关系,属于中档题.

练习册系列答案
相关题目
 已知点A(1,0)、B(2,0),点C在y轴的正半轴上,求∠ACB取最大值时,C点的坐标.
已知点A(1,0)、B(2,0),点C在y轴的正半轴上,求∠ACB取最大值时,C点的坐标.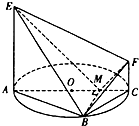 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.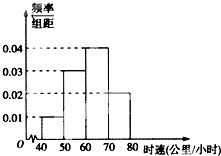 已知某一段公路限速60公里/小时,现抽取200辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这200辆汽车中在该路段没有超速的有
已知某一段公路限速60公里/小时,现抽取200辆通过这一段公路的汽车的时速,其频率分布直方图如图所示,则这200辆汽车中在该路段没有超速的有